Number system and digital device details

আইসিটি অধ্যায়-৩.১ : সংখ্যাপদ্ধতি ও ডিজিটাল ডিভাইস
সংখ্যা পদ্ধতিঃ-সংখ্যা গণনা বা হিসাব করার জন্য বিভিন্ন প্রতীক বা সাংকেতিক চিহ্ন ব্যবহৃত হয়। এই সকল প্রতীক লেখার নিয়ম সমূহকেই সংখ্যা পদ্ধতি বলা হয়। অর্থাৎ যে পদ্ধতির মাধ্যমে সংখ্যা প্রকাশ এবং গণনা করা হয়, তাহাই সংখ্যা পদ্ধতি নামে পরিচিত।
সংখ্যা পদ্ধতি দুই প্রকার। যথা-
নন – পজিশনাল সংখ্যা পদ্ধতিঃ- এই ধরনের সংখ্যা পদ্ধতিতে ব্যবহৃত সংখ্যার অংক সমূহের কোনো স্থানীয় মান থাকে না। শুধু সংখ্যার নিজস্ব মান থাকে। যেমন- হায়ারোগ্লিফিক্স(Hieroglyphics), ম্যায়ন(Mayan) ইত্যাদি।
পজিশনাল সংখ্যা পদ্ধতিঃ- যে পদ্ধতিতে সংখ্যার মান ব্যবহৃত অংকসমূহের পজিশন বা অবস্থানের উপর নির্ভর করে তাকে পজিশন্যাল সংখ্যা পদ্ধতি বলে। অংকসমূহের অবস্থানের উপর ভিত্তি করে এই ধরনের সংখ্যা পদ্ধতিতে সংখ্যার মান নির্ণয় করা হয়।
পজিশনাল সংখ্যা পদ্ধতি চার ধরণের তা হলোঃ
1.বাইনারী সংখ্যা পদ্ধতি
2.দশমিক/ডেসিম্যাল সংখ্যা পদ্ধতি
3.অকট্যাল সংখ্যা পদ্ধতি
4.হেক্সাডেসিম্যাল সংখ্যা পদ্ধতি
দশমিক/ডেসিম্যাল সংখ্যা পদ্ধতি
প্রাত্যহিক বাস্তব জীবনে হিসাব নিকাশ করার জন্য আমরা যে সংখ্যা পদ্ধতি ব্যবহার করি তা দশমিক সংখ্যা পদ্ধতি। এর ভিত্তি 10 অর্থাত এই পদ্ধতিতে 0 হতে 9 পর্যন্ত মোট 10টি সংখ্যা প্রতীক রয়েছে।
ডিজিটাল ইলেকট্রনিক্সের হিসাব নিকাশের সময় কখনো কখনো দশমিক সংখ্যার সাথে সাফিক্স হিসাবে এর ভিত্তি লিখে প্রকাশ করা হয়, এর মাধ্যমে বুঝা যায় সংখ্যাটি দশমিক সংখ্যা। যেমনঃ (9347)10 এখানে 9347 হলো ডেসিম্যাল সংখ্যা এবং 10 হলো এর ভিত্তি যার মাধ্যমে বুঝা যাচ্ছে সংখ্যাটি দশমিক পদ্ধতির সংখ্যা।
দ্বিমিক/বাইনারী সংখ্যা পদ্ধতি
এই সংখ্যা পদ্ধতির ভিত্তি 2 অর্থাত এই পদ্ধতিতে 0 এবং 1 মোট 2টি সংখ্যা প্রতীক রয়েছে। ডিজিটাল ইলেকট্রনিক্সের হিসাব নিকাশের সময় কখনো কখনো দ্বিমিক সংখ্যার সাথে সাফিক্স হিসাবে এর ভিত্তি লিখে প্রকাশ করা হয়, এর মাধ্যমে বুঝা যায় সংখ্যাটি দ্বিমিক সংখ্যা। যেমনঃ (101001)2 এখানে 101001 হলো ডেসিম্যাল সংখ্যা এবং 2 হলো এর ভিত্তি যার মাধ্যমে বুঝা যাচ্ছে সংখ্যাটি দ্বিমিক বা বাইনারী পদ্ধতির সংখ্যা।
অকট্যাল সংখ্যা পদ্ধতি
এই সংখ্যা পদ্ধতির ভিত্তি 8 অর্থাত এই পদ্ধতিতে 0 হতে 7 পর্যন্ত মোট 8টি সংখ্যা প্রতীক রয়েছে। ডিজিটাল ইলেকট্রনিক্সের হিসাব নিকাশের সময় কখনো কখনো অকট্যাল সংখ্যার সাথে সাফিক্স হিসাবে এর ভিত্তি লিখে প্রকাশ করা হয়, এর মাধ্যমে বুঝা যায় সংখ্যাটি অকট্যাল সংখ্যা। যেমনঃ (756)8 এখানে 756 হলো অকট্যাল সংখ্যা এবং 8 হলো এর ভিত্তি যার মাধ্যমে বুঝা যাচ্ছে সংখ্যাটি অকট্যাল পদ্ধতির সংখ্যা।
হেক্সাডেসিম্যাল সংখ্যা পদ্ধতি
এই সংখ্যা পদ্ধতির ভিত্তি 16 অর্থাত এই পদ্ধতিতে 0 হতে 9 পর্যন্ত মোট 10টি সংখ্যা প্রতীক এবং সেই সাথে A, B, C, D, E, F এই 6টি বর্ণ প্রতীক রয়েছে। ডিজিটাল ইলেকট্রনিক্সের হিসাব নিকাশের সময় কখনো কখনো হেক্সাডেসিম্যাল সংখ্যার সাথে সাফিক্স হিসাবে এর ভিত্তি লিখে প্রকাশ করা হয়, এর মাধ্যমে বুঝা যায় সংখ্যাটি হেক্সাডেসিম্যাল সংখ্যা। যেমনঃ (5C7F)16 এখানে 5C7F হলো হেক্সাডেসিম্যাল সংখ্যা এবং 16 হলো এর ভিত্তি যার মাধ্যমে বুঝা যাচ্ছে সংখ্যাটি হেক্সাডেসিম্যালপদ্ধতির সংখ্যা।
সংখ্যা পদ্ধতির রূপান্তর- এক ধরনের সংখ্যা পদ্ধতি থেকে অন্য আরেক ধরনের সংখ্যা পদ্ধতির সমকক্ষ মান নির্ণয় করাকে সংখ্যা পদ্ধতির রূপান্তর বলা হয়। আমাদের দৈনন্দিন জীবনে বিভিন্ন হিসেব করার জন্য দশমিক সংখ্যা পদ্ধতি ব্যবহার করলেও কম্পিউটার বাইনারি, অক্ট্যাল এবং হেক্সাডেসিমেল সংখ্যা পদ্ধতি নিয়ে কাজ করে থাকে।
Type-1: দশমিক থেকে বাইনারি, অক্ট্যাল এবং হেক্সাডেসিমেল-এ রূপান্তর
রূপান্তর পদ্ধতিঃ–
যেকোনো দশমিক সংখ্যার দুইটি অংশ (পূর্ণ অংশ এবং ভগ্নাংশ) থাকতে পারে।
পুর্নাংশের ক্ষেত্রে-
- যে দশমিক পূর্ণ সংখ্যাকে পরিবর্তন করতে হবে তাকে কাঙ্ক্ষিত সংখ্যা পদ্ধতির বেজ বা ভিত্তি দিয়ে ভাগ করতে হবে। যেমন- বাইনারি সংখ্যা হলে তার ভিত্তি ২, অক্ট্যাল হলে ৮ এবং হেক্সাডেসিমেল হলে ১৬ দিয়ে ভাগ করতে হবে। পাশাপাশি ভাগশেষটিকে সংরক্ষণ করতে হবে।
- উপরের ধাপে প্রাপ্ত ভাগফলকে আবার কাঙ্ক্ষিত সংখ্যা পদ্ধতির বেজ বা ভিত্তি দিয়ে ভাগ করতে হবে এবং ভাগশেষটিকে সংরক্ষণ করতে হবে।
- প্রক্রিয়াটি ততক্ষণ পর্যন্ত চলবে যতক্ষণ ভাগফল শূন্য না হয়েছে।
- সর্বশেষে প্রাপ্ত ভাগফল থেকে অর্থাৎ নিচের দিক থেকে উপরের দিকে সাজিয়ে ভাগশেষ সমূহ লিখলে রুপান্তরিত সংখ্যার পুর্নাংশ পাওয়া যায়।
ভগ্নাংশের ক্ষেত্রে-
- যে দশমিক ভগ্নাংশ সংখ্যাকে পরিবর্তন করতে হবে তাকে কাঙ্ক্ষিত সংখ্যা পদ্ধতির বেজ বা ভিত্তি দিয়ে গুণ করতে হবে। যেমন- বাইনারি সংখ্যা হলে তার ভিত্তি ২, অক্ট্যাল হলে ৮ এবং হেক্সাডেসিমেল হলে ১৬ দিয়ে ভাগ করতে হবে। গুনফলে প্রাপ্ত পুর্নাংশটিকে সংরক্ষণ করতে হবে।
- উপরের ধাপে প্রাপ্ত গুনফলের ভগ্নাংশটিকে আবার কাঙ্ক্ষিত সংখ্যা পদ্ধতির বেজ বা ভিত্তি দিয়ে গুণ করতে হবে এবং প্রাপ্ত পুর্নাংশটিকে সংরক্ষণ করতে হবে।
- এই গুণ করার প্রক্রিয়াটি ততক্ষণ পর্যন্ত চলবে যতক্ষণ গুনফলের ভাগ্নাংশের মান শূন্য না হয়।
- র্যাডিক্স পয়েন্টের বামে প্রাপ্ত পূর্ণ সংখ্যাগুলোকে উপরের দিক থেকে নিচের দিকে সাজিয়ে লিখলে রুপান্তরিত সংখ্যার ভগ্নাংশ পাওয়া যাবে।
উদাহরণ-১ঃ (17.125)10 সংখ্যাটিকে বাইনারিতে রূপান্তর কর।
উত্তরঃ-
সুতরাং (17.125)10 সংখ্যাটির বাইনারি (10001.001)2
উদাহরণ-২ (17.125)10 সংখ্যাটিকে অক্ট্যালে রূপান্তর কর।
উত্তরঃ- নিজে চেষ্টা কর।
উদাহরণ-৩ (17.125)10 সংখ্যাটিকে হেক্সাডেসিমেলে রূপান্তর কর।
উত্তরঃ- নিজে চেষ্টা কর।
Type-2: বাইনারি, অক্ট্যাল এবং হেক্সাডেসিমেল থেকে দশমিক-এ রূপান্তর
রূপান্তর পদ্ধতিঃ– যেকোনো সংখ্যা পদ্ধতি থেকে দশমিক সংখ্যা পদ্ধতিতে রুপান্তরের ক্ষেত্রে দুইটি অংশ (পূর্ণ অংশ এবং ভগ্নাংশ)থাকতে পারে।
পুর্নাংশের ক্ষেত্রে-
- সংখ্যাটির LSB (List Significant Bit) বিট থেকে শুরু করে MSB (Most Significant Bit) বিট পর্যন্ত প্রতিটি অংককে পর্যায়ক্রমে Base n দ্বারা গুন করতে হবে (যেমন- বাইনারি সংখ্যার ক্ষেত্রে 2 n , অক্ট্যাল সংখ্যার ক্ষেত্রে 8 n , হেক্সাডেসিমেল সংখ্যার ক্ষেত্রে 16n ইত্যাদি।
- এখানে Base=সংখ্যা পদ্ধতির ভিত্তি এবং n=0, 1, 2, 3, 4,………
- অতঃপর গুণগুলোর যোগফল নির্ণয় করতে হবে।
- প্রাপ্ত যোগফলই হবে প্রদত্ত সংখ্যাটির (পূর্ণ সংখ্যা) সমতূল্য দশমিক মান।
সূত্রঃ- (…abc)Base=….+(a*Base2)+(b*Base1)+(c*Base0)
ভগ্নাংশের ক্ষেত্রে-
- সংখ্যাটির MSB (Most Significant Bit) বিট থেকে শুরু করে LSB (List Significant Bit) বিট পর্যন্ত প্রতিটি অংককে পর্যায়ক্রমে Base -n দ্বারা গুন করতে হবে (যেমন- বাইনারি সংখ্যার ক্ষেত্রে 2 -n , অক্ট্যাল সংখ্যার ক্ষেত্রে 8-n , হেক্সাডেসিমেল সংখ্যার ক্ষেত্রে 16-n ইত্যাদি।
- এখানে Base=সংখ্যা পদ্ধতির ভিত্তি এবং n=0, 1, 2, 3, 4,………
- অতঃপর গুণগুলোর যোগফল নির্ণয় করতে হবে।
- প্রাপ্ত যোগফলই হবে প্রদত্ত সংখ্যাটির (ভগ্নাংশের সংখ্যা) সমতূল্য দশমিক মান।
সূত্রঃ- (…abc)Base= (a*Base-1)+(b*Base-2)+(c*Base-3)+….
উদাহরণ-১: (11.101)2 সংখ্যাটিকে দশমিক সংখ্যা পদ্ধতিতে রূপান্তর কর।
উত্তরঃ- সূত্রঃ- (abc.xyz)Base=(a*Base2)+(b*Base1)+(c*Base0)+(x*Base-1)+(y*Base-2)+(z*Base-3)
দেওয়া আছে,
(11.101)2
= (1*21)+(1*20)+(1*2-1)+(0*2-2)+(1*2-3)
= 2 + 1 + 0 + .125
= 3.125
Answer:- (3.125)10
উদাহরণ-২: (ABBA.DADA)16 সংখ্যাটিকে দশমিক সংখ্যা পদ্ধতিতে রূপান্তর কর।
উত্তরঃ- সূত্রঃ- (abc.xyz)Base=(a*Base2)+(b*Base1)+(c*Base0)+(x*Base-1)+(y*Base-2)+(z*Base-3)
দেওয়া আছে,
(ABBA.DADA)16= (A*163)+(B*162)+(B*161)+(A*160)+(D*16-1)+(A*16-2)+(D*16-3)+(A*16-4)
বাকি অংশ নিজে চেষ্টা কর।
উদাহরণ-৩: (BADDA.ADDA)16 সংখ্যাটিকে দশমিক সংখ্যা পদ্ধতিতে রূপান্তর কর।
উত্তরঃ- নিজে চেষ্টা কর।
উদাহরণ-৪: (3775.5671)8 সংখ্যাটিকে দশমিক সংখ্যা পদ্ধতিতে রূপান্তর কর।
উত্তরঃ-নিজে চেষ্টা কর।
Type-3: বাইনারি থেকে অক্ট্যাল এবং হেক্সাডেসিমেল-এ রূপান্তর, অক্ট্যাল এবং হেক্সাডেসিমেল থেকে বাইনারিতে রুপান্তর, অক্ট্যাল এবং হেক্সাডেসিমেল-এ আবার হেক্সাডেসিমেল থেকে অক্ট্যাল সংখ্যা পদ্ধতিতে রুপান্তর
বাইনারি সংখ্যাকে অক্টাল সংখ্যায় রূপান্তর:
১। যেহেতু ৩-বিটের বাইনারি সংখ্যা দিয়ে একটি অক্টাল ডিজিট তৈরি হয়, তাই সেই সংখ্যাটির LSB থেকে MSB অর্থাৎ ডান থেকে বাম দিকে ৩-বিট করে পৃথক করে নিতে হবে।
২। ৩-বিটের কম হলে বাম পার্শ্বে প্রয়োজনীয় সংখ্যক শুন্য বসিয়ে ৩-বিট পূর্ণ করতে হবে।
৩। অতপর প্রতিটি ৩-বিট অংশের আলাদা আলাদা ভাবে ডেসিমেল মান নির্ণয় করতে হবে।
ভগ্নাংশের ক্ষেত্রে-
১। যেহেতু ৩-বিটের বাইনারি সংখ্যা দিয়ে একটি অক্টাল ডিজিট তৈরি হয়, তাই সেই সংখ্যাটির MSB থেকে LSB অর্থাৎ বাম থেকে ডান দিকে ৩-বিট করে পৃথক করে নিতে হবে।
২। ৩-বিটের কম হলে ডান পার্শ্বে প্রয়োজনীয় সংখ্যক শুন্য বসিয়ে ৩-বিট পূর্ণ করতে হবে।
৩। অতপর প্রতিটি ৩-বিট অংশের আলাদা আলাদা ভাবে ডেসিমেল মান নির্ণয় করতে হবে।
১। (1101001)2 কে অক্টাল সংখ্যা পদ্ধতিতে রূপান্তর কর।
২। (.1010011)2 কে অক্টাল সংখ্যা পদ্ধতিতে রূপান্তর কর।
বাইনারি সংখ্যাকে হেক্সাডেসিমেল সংখ্যায় রূপান্তরঃ
পূর্ণ সংখ্যার ক্ষেত্রে-
১। যেহেতু ৪-বিটের বাইনারি সংখ্যা দিয়ে একটি হেক্সাডেসিমেল ডিজিট তৈরি হয়, তাই সেই সংখ্যাটির LSB থেকে MSB অর্থাৎ ডান থেকে বাম দিকে ৪-বিট করে পৃথক করে নিতে হবে।
২। ৪-বিটের কম হলে বাম পার্শ্বে প্রয়োuuজনীয় সংখ্যক শুন্য বসিয়ে ৪-বিট পূর্ণ করতে হবে।
৩। অতপর প্রতিটি ৪-বিট অংশের আলাদা আলাদা ভাবে ডেসিমেল মান নির্ণয় করতে হবে।
ভগ্নাংশের ক্ষেত্রে-
১। যেহেতু ৪-বিটের বাইনারি সংখ্যা দিয়ে একটি হেক্সাডেসিমেল ডিজিট তৈরি হয়, তাই সেই সংখ্যাটির MSB থেকে LSB অর্থাৎ বাম থেকে ডান দিকে ৪-বিট করে পৃথক করে নিতে হবে।
২। ৪-বিটের কম হলে ডান পার্শ্বে প্রয়োজনীয় সংখ্যক শুন্য বসিয়ে ৪-বিট পূর্ণ করতে হবে।
৩। অতপর প্রতিটি ৪-বিট অংশের আলাদা আলাদা ভাবে ডেসিমেল মান নির্ণয় করতে হবে।
১। (1101101)2 কে অক্টাল সংখ্যা পদ্ধতিতে রূপান্তর কর।
২। (.1010011)2 কে অক্টাল সংখ্যা পদ্ধতিতে রূপান্তর কর।
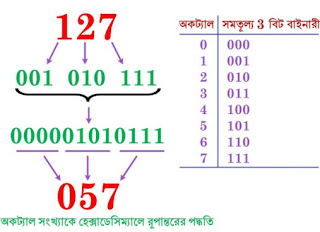
অক্টাল সংখ্যাকে বাইনারি সংখ্যায় রূপান্তর:
১। অক্ট্যাল সংখ্যার প্রতিটি ডিজিটের আলাদা আলাদা বাইনারি মান নির্ণয় করতে হবে।
২। যেহেতু ৩-বিট দিয়ে একটি অক্ট্যাল ডিজিট প্রকাশ করা হয়। তাই কোন অক্ট্যাল সংখ্যার প্রতিটি ডিজিটের বাইনারি মান ৩-বিটের কম হলে বাম পার্শ্বে প্রয়োজনীয় সংখ্যক শুন্য বসিয়ে ৩-বিট পূর্ণ করতে হবে।
৩। অবশেষে প্রাপ্ত বাইনারি মান গুলিকে পাশাপাশি সাজিয়ে লিখলে অক্ট্যাল সংখ্যাটির সমতূল্য বাইনারি সংখ্যা পাওয়া যাবে।
১। (127)8 কে বাইনারি সংখ্যা পদ্ধতিতে রূপান্তর কর।
২। (.7125)8 কে বাইনারি সংখ্যা পদ্ধতিতে রূপান্তর কর।
হেক্সাডেসিমেল সংখ্যাকে বাইনারি সংখ্যায় রূপান্তরঃ
১। হেক্সাডেসিমেল সংখ্যার প্রতিটি ডিজিটের আলাদা আলাদা বাইনারি মান নির্ণয় করতে হবে।
২। যেহেতু ৪-বিট দিয়ে একটি হেক্সাডেসিমেল ডিজিট প্রকাশ করা হয়। তাই কোন হেক্সাডেসিমেল সংখ্যার প্রতিটি ডিজিটের বাইনারি মান ৪-বিটের কম হলে বাম পার্শ্বে প্রয়োজনীয় সংখ্যক শুন্য বসিয়ে ৪-বিট পূর্ণ করতে হবে।
৩। অবশেষে প্রাপ্ত বাইনারি মান গুলিকে পাশাপাশি সাজিয়ে লিখলে হেক্সাডেসিমেল সংখ্যাটির সমতূল্য বাইনারি সংখ্যা পাওয়া যাবে।
১। (D218)16 কে বাইনারি সংখ্যা পদ্ধতিতে রূপান্তর কর।
২। (.1C39)16 কে বাইনারি সংখ্যা পদ্ধতিতে রূপান্তর কর।
হেক্সাডেসিম্যাল হতে অকট্যাল রূপান্তরঃ
১। হেক্সাডেসিম্যাল সংখ্যাটিকে সমতূল্য বাইনারী সংখ্যায় রূপান্তর করতে হবে।
২। প্রাপ্ত বাইনারী সংখ্যাটিকে সমতূল্য অকট্যালে রূপান্তর করলেই কাংখিত অকট্যালে সংখ্যা পাওয়া যাবে।
চিত্র হতে পাই (12A)16 = 0452 = (452)8। প্রথমে হেক্সাডেসিম্যাল সংখ্যাটির প্রতিটি অংককে 4 বিটের বাইনারী সংখ্যায় রূপান্তর করা হয়। অতঃপর বাইনারী অংকগুলিকে পাশাপাশি সাজিয়ে তা হতে 3 ডিজিটের বাইনারী গ্রুপে তৈরী করা হয় এবং উক্ত প্রতিটি গ্রুপকে সমতূল্য ডেসিম্যাল সংখ্যা দ্বারা প্রতিস্থাপন করলে প্রাপ্ত সংখ্যাটি কাংখিত অকট্যাল সংখ্যা।
অকট্যাল হতে হেক্সাডেসিম্যাল রূপান্তরঃ
১। অকট্যাল সংখ্যাটিকে সমতূল্য বাইনারী সংখ্যায় রূপান্তর করতে হয়।
২। প্রাপ্ত বাইনারী সংখ্যাটিকে হেক্সাডেসিম্যালে রূপান্তর করতে হয়।
বাইনারী যোগঃ
প্রচলিত বাইনারী যোগের নিয়ম –
1+1=0 এবং হাতে থাকে 1 যা পরের সারিতে (বামে) যোগ করতে হবে।
0+1=1
0+0=0
এখন উপরোক্ত নিয়ম অনুযায়ী যদি নিচের বড় বাইনারী যোগটি করতে হয় তাহলে হাতে কত থাকছে এটা অনেক সময় ভূল হতে পারে এবং সময় সাপেক্ষ। কিন্তু যদি আমরা ডানদিকের প্রথম কলামের যোগ করি অর্থাৎ ডানদিকের প্রথম কলামে মোট 5 টি বিট রয়েছে একে বাইনারীর ভিত্তি 2 দ্বারা ভাগ করে ভাগফলটি হাতে রাখি এবং অবশিষ্ট 1 যোগফলের ঘরে অর্থাৎ প্রথম কলামের নিচে নামিয়ে দিই এবং হাতের 2 বা দুইটি বিট পরের কলামের সংগে যোগ করি একই নিয়মে মোট বিট সংখ্যাকে বাইনারী বেস্ 2 দ্বারা ভাগ করে আবারও ভাগফল হাতে রাখি এবং অবশিষ্ট যোগের কলামে বা সারিতে নামিয়ে দিই তাহলে যোগফল মিলে যাবে। একই নিয়মে পরের কলামের বাইনারী বিটগুলি সহজে যোগ করে ফেলতে পারি। সবশেষে যখন বামদিকে আর কোন যোগ করার মত কলাম থাকবে না তখন ভাগফল যদি বেসের বা ভিত্তির চেয়ে ছোট হয় তবে সরাসরি তা যোগফলের ঘরে নামাতে হবে আর যদি বড় তাহলে পুনরায় বেস দ্বারা ভাগ করে উপরের নিয়মে নামিয়ে আসতে হবে।
নিচের বাইনারী যোগটি উদাহরণ হিসাবে দেওয়া হল –
1 1 1 1 1
1 0 1 0 1
1 1 1 1 1
1 0 1 1 1
1 1 1 1 1
1 0 0 0 1 0 0 1
যে নিয়মে বেস দ্বারা ভাগ করব – সরাসরি দশমিক পদ্ধতির মত এখানে বাইনারী বেস বা ভিত্তি 2দ্বারা প্রথম বামদিকের কলামের বিটগুলির যোগফল 5 কে ভাগ করেছি –
অর্থাৎ 2 ) 5 ( 2 ভাগফল অর্থাৎ বাইনারীর দুইটি বিট।
4
1 অবশিষ্ট উপরোক্ত নিয়মে বাইনারী যোগ করলে ভূল হবার কোন সম্ভাবনা নেই।
বাইনারী বিয়োগঃ প্রচলিত বাইনারী বিয়োগের নিয়ম-
1-1=0
1-0=1
0-1=1
পরের বাঁ দিকের কলাম বা সারি থেকে 1 ধার নিতে হবে ।
কিন্তু বাইনারী বিয়োগ এখানে যেভাবে দশমিক পদ্ধতির বিয়োগ করে থাকি সেভাবেই সহজে করতে পারি। যেমন দশমিকের ক্ষেত্রে উপরের উপরের সংখ্যাটি যদি নিচের সংখ্যাটি অপেক্ষা ছোট থাকে তাহলে আমরা উপরের সাথে ঐ সংখ্যা পদ্ধতির বেস বা ভিত্তি কত সেটি ধার নিই যেমন এখানে 10 ধার নিই এবং পরের কলামের নিচে যে বেসটি ধার নেওয়া হয়েছে অর্থাৎ 1 বেস সেটি নিচে যোগ করে দিই। পরের সারিতে আবারও যদি উপরের সংখ্যাটি ছোট হয় তখন একইভাবে বেস ধার নিই।
বাইনারী বিয়োগের উদাহরণ-
1 1 0 0
1 0 1 1
(0 0 0 1)2
বিয়োগটির ক্ষেত্রে ডানদিকের প্রথম কলামে উপরের বিটটি 0 অর্থাৎ নিচেরটির বিটটির চেয়ে ছোট সেইহেতু বাইনারী বেস অর্থাৎ 2 উপরে যোগ করে নিব তাহলে নিচের 1 ওর সাথে বিয়োগ করলে 1 নামবে এবং হাতে একটি বেস থাকবে যা পরের কলামের নিচে যোগ করতে হবে এবং উপরে আবারাও ছোট হলে বেস যোগ করে নিতে হবে একই নিয়মে চলতে থাকবে এবং বিয়োগ সহজে মিলে যাবে।
বাইনারী গুনঃ বাইনার গুন দশমিক গুণের অনুরূপ- উদাহরণ-
1 1 0 1 1 × 1 1 1 1 1 0 1 1 1 1 0 1 1 × 1 1 0 1 1 × . 1 0 1 1 1 1 0 1
উপরোক্ত বাইনারী গুণটি করার পর যোগের সময় আগের নিয়ম অনুসরণ করা হয়েছে যা অতি সহজে সম্ভব হয়েছে।
অকটাল যোগঃ উদাহরণ-
7 6 5 4 3 4 6 7 2 1 3 0 7 2 3 5 6 1 5 3 (2 5 4 5 6 2)8
উপরের অকটাল যোগটির ক্ষেত্রেও আমরা দশমিক যোগের পদ্ধতির অনুরূপ পদ্ধতি অনুসরণ করেছি। ডানদিকের প্রথম কলামে আছে 3+1+3+3=10 অর্থাৎ যোগ করে পেয়েছি 10 যাকে অকটালের বেস বা ভিত্তি 8 দ্বারা ভাগ করেছি এতে ভাগফল 1 হাতে রেখেছি এবং অবশিষ্ট 2 যোগফলের ঘরে নামিয়ে দিয়েছি এভাবে পরবর্তী কলামগুলোর যোগ করেছি এবং হাতে থাকা অংকটি তার সাথে যোগ করে অকটাল বেস দ্বারা ভাগ করে ভাগফল হাতে রেখে অবশিষ্ট যোগফলের নামিয়ে যোগ করতে করতে বামের কলামগুলোর যোগ সম্পন্ন করেছি। এভাবে শেষের ঘরটির ভাগফল যখন বেসের চেয়ে ছোট হয়েছে তখন সরাসরি তা যোগফলের ঘরে বসিয়ে যোগের কাজ সম্পন্ন করেছি। এতে ভূল হবার কোনরকম সম্ভবনা নেই।
অকটাল বিয়োগঃ
7 3 2 – 4 5 6 ( 2 5 4)8
উপরের অকটাল বিয়োগটির ক্ষেত্রে আমরা দশমিকের মত পদ্ধতি অনুসরণ করতে পারি, ডানদিকের প্রথম কলামে যেহেতু উপরের অংকটি ছোট অর্থাৎ উপরে 2এবং নিচে বড় 6 এক্ষেত্রে বিয়োগ করার জন্য উপরেরটির সাথে অকটালের বেস বা ভিত্তি 8 যোগ করে নিচেরটির সাথে বিয়োগ করলে বিয়োগফল হবে 4, সেটি বিয়োগফলের ঘরে বসিয়ে দিতে হবে এবং একটি বেস ধার নেওয়ার কারনে পরবর্তী কলামের নিচে ঐ 1 যোগ করে নিতে হবে, আবারও যদি উপরের অংকটি ছোট থাকে তাহলে একই নিয়মে বেস যোগ করে তার সাথে নিচেরটি বিয়োগ করলে বিয়োগফল মিলে যাবে।
অক্টাল গুনঃ
7 5 6 ×5 4 3 . 2 7 1 2 3 6 7 0 × 4 6 4 6 × . (5 2 6 4 1 2)8
উপরের গূনটি কি করে করলাম। এখানে খেয়াল রাখতে হবে অংকটি অকটাল পদ্ধতির। তাই এখানে অকটাল বেস ব্যবহার করতে হবে। প্রথমে 6 কে 3 দ্বারা গুন করেছি এবং পেয়েছি 18 যাকে আবার অকটালের বেস 8 দ্বারা ভাগ করেছি ফলে ভাগফল হয়েছে 2 এবং অবশিষ্ট থেকেছে 2 যা গুনফলের ঘরে বসিয়েছি। দশমিকের ক্ষেত্রে 18 হলে 10দ্বারা ভাগ করতাম তাতে হাতে থাকত 1 এবং অবশিষ্ট 8 গুনফলের ঘরে নামিয়ে দিতাম। এরপর 5কে 3 দ্বারা গুন করেছি এবং হাতের 2 এর সাথে যোগ করে আবারও 8 দ্বারা ভাগ করে ভাগফল হাতে রেখেছি এবং অবশিষ্ট গুনফলের ঘরে বসিয়েছি। সবশেষে অকটাল পদ্ধতির যোগ করে গুনফলটি সম্পন্ন করেছি।
হেক্সাডেসিমাল যোগঃ হেক্সাডেসিমালের বেস বা ভিত্তি হচ্ছে 16 যথা 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F. একই পদ্ধতি অনুসরণ করে আমরা হেক্সাডেসিমাল যোগ করতে পারি- উদাহরণ-
A B C A B C . A B C . (2 0 3 4)16
উপরের যোগটির ক্ষেত্রে ডানদিকের প্রথম কলামে যেহেতু C = 12 অতএবC+C+C = 36 কে হেক্সাডেসিমাল বেস 16 দ্বারা ভাগ করে ভাগফলটি অর্থাৎ 2 হাতে রাখব এবং অবশিষ্ট 4 যোগফলের ঘরে নামিয়ে দিব এবং পরবর্তী ঘরের তিনটি B যোগ করে তার সাথে হাতে রাখা 2 যোগ করে 35 যাকে আবার 16 দ্বারা ভাগ করে অবশিষ্ট 3 যোগফলের ঘরে নামিয়ে দিয়েছি। পরবর্তী ঘরের তিনটি A যোগ করে হয়েছে 30 যার সাথে হাতে রাখা 2 যোগ করে যার পেয়েছি 32। এখন একে হেক্সাডেসিমাল বেস 16 দ্বারা ভাগ করে ভাগফল পেয়েছি 2 এবং অবশিষ্ট 0 যা যোগফলের ঘরে বসিয়েছি এবং ভাগফলের 2 বা হাতে থাকা 2 যা বেসের চেয়ে ছোটহওয়ায় তা যোগফলের ঘরে নামিয়ে দিয়ে যোগর কাজ সমাপ্ত করেছি। এই পদ্ধতিতে অতি তাড়াতাড়ি যে কোন হেক্সাডেসিমাল যোগ করা যায়। তবে মনে রাখতে হবে যে- 10 অবশিষ্ট থাকলে A, 11 থাকলে B, 12 থাকলে C, 13 থাকলে D, 14 থাকলে E এবং 15 থাকলে F যোগফলের ঘরে নামাতে হবে। তবে ভাগফলের ক্ষেত্রে যেটা আসবে সেটা সরাসরি হাতে রাখতে হবে ঐটির ক্ষেত্রে মান বসানোর দরকার নেই কারণ ওটি হচ্ছে কতটি বেস তার সংখ্যা।
হেক্সাডেসিমাল বিয়োগঃ হেক্সাডেসিমাল বিয়োগের ক্ষেত্রে একই নিয়ম অর্থাৎ দশমিকে যেভাবে তার বেস উপরে ছোট হলে যোগ করতে হয় এখানেও ঠিক তেমনিভাবে করতে হবে। উদাহরণ-
7 D B . – 3 F E . 3 D D
উপরের উদাহরণটিতে দেখা যায় ডানদিকের প্রথম কলামের উপরে রয়েছে B অর্থাৎ 11 এবং নিচে রয়েছে E অর্থাৎ 14, যেহেতু উপরেরটি নিচেরটির চেয়ে ছোট সেইহেতু হেক্সাডেসিমালের বেস অর্থাৎ 16 উপরেরটির সাথে যোগ করতে হবে তাতে পাওয়া যাবে মোট 27 এবং এ থেকে 14 বিয়োগ করলে পাওয়া যাবে 13 যা সমান হবে Dএকে বিয়োগফলের ঘরে বসাতে হবে এবং পরবর্তী ঘরের নিচেরটির সাথে দশমিক পদ্ধতির অনুরূপ 1 অর্থাৎ একটি বেস যোগ করতে হবে আবারও যদি উপরেরটি নিচেরটির অপেক্ষা ছোট হয় তবে একই পদ্ধতি অনুসরণ করে বিয়োগের কাজ সম্পূর্ণ করতে হবে।
হেক্সাডেসিমাল গুনঃ নিচের গুনটি হেক্সাডেসিমাল পদ্ধতিতে করা হয়েছে-
A B × A B . 7 5 9 6 A E × . ( 7 2 3 9)16
উপরের হেক্সাডেসিমাল গুণের ক্ষেত্রে প্রথমে B×B গুণ করেছি অর্থাৎ 11×11 = 121 গুণফলকে হেক্সাডেসিমাল বেস 16 দ্বারা ভাগ করে ভাগফল 7 হাতে রেখেছি এবং অবশিষ্ট 9 গুণফলের ঘরে নামিয়েছি, এরপর A×B গুণ হাতে থাকা 7 যোগ করে আবারও বেস দ্বারা ভাগ করে ভাগফল হাতে রেখে অবশিষ্ট গুণফলের ঘরে নামিয়ে হাতে রাখা অংকটি বেসের চেয়ে কম হওয়ায় সরাসরি নামিয়ে প্রথম লাইনটির গুণ সম্পূর্ণ করেছি। একইভাবে দ্বিতীয় লাইনটির গুণের কাজ সম্পূর্ণ করেছি। এরপর হেক্সাডেসিমাল পদ্ধতি অনূসরণ করে যোগের কাজ সম্পূর্ণ করেছি।
বিঃ দ্রঃ উপরোক্ত পদ্ধতি অনুসরণ করে যদি বিভিন্ন সংখ্যা পদ্ধতির যোগ ইত্যাদি করা যায় তবে তাতে ভূল সম্ভবনা কম থাকবে আশাকরি এবং সহজে সম্পন্ন করা যাবে।
কমপ্লিমেন্ট বা পূরক এর ধারণাঃ
কোন কিছুর সংখ্যা বা পরিমান যা একটি নির্দিষ্ট পরিমান পূর্ণ করতে প্রয়োজন হয় তাকে পূরক বা কমপ্লিমেন্ট বলা হয়। অন্য কথায় পূরক বলতে পূর্ণ পরিমান হতে ঘাটতি বুঝায়। ডিজিটাল ইলেকট্রনিক্সের ভাষায় কোন একটি অংক হতে ঐ সংখ্যা পদ্ধতির ভিত্তি পূরণ করতে যে পরিমান ঘাটতি থাকে তাই উক্ত অংকের পূরক। যেমনঃ দশমিক পদ্ধতিতে 7 এর পূরক 3 কারন দশমিক সংখ্যা পদ্ধতির ভিত্তি 10 পূর্ণ করতে 7 এর নিকট এখনো (10–7)10=3 ঘাটতি রয়েছে । সুতরাং 7 এর 10’s কমপ্লিমেন্ট হলো 3 । আবার বাইনারী সংখ্যা পদ্ধতিতে 1 এর 2’s কমপ্লিমেন্ট হলো 1 কারণ বাইনারী সংখ্যা পদ্ধতির ভিত্তি 2 পূর্ণ করতে 1 এর নিকট এখনো (10–1)2=1 ঘাটতি রয়েছে।
কমপ্লিমেন্ট বা পূরকের প্রকারঃ
ডিজিটাল ইলেকট্রনিক্সে দুই ধরণের কমপ্লিমেন্ট বা পূরকের ব্যবহার দেখা যায়ঃ
১। r’s কমপ্লিমেন্ট এবং
২। (r – 1)’s কমপ্লিমেন্ট
এখানে r হলো সংখ্যা পদ্ধতির Radix বা ভিত্তি। যদি সংখ্যা পদ্ধতিটি বাইনারী হয় তবে তার ভিত্তি 2 এবং এই সংখ্যা পদ্ধতির পূরক দুটি হবে 2’s কমপ্লিমেন্ট এবং (2 – 1)’s বা 1’s কমপ্লিমেন্ট। যদি সংখ্যা পদ্ধতিটি অকট্যাল হয় তবে তার ভিত্তি 8 এবং এই সংখ্যা পদ্ধতির পূরক দুটি হবে 8’s কমপ্লিমেন্ট এবং (8–1)’s বা 7’s কমপ্লিমেন্ট। অনুরূপভাবে যদি সংখ্যা পদ্ধতিটি ডেসিম্যাল হয় তবে তার ভিত্তি 10 এবং এই সংখ্যা পদ্ধতির পূরক দুটি হবে 10’s কমপ্লিমেন্ট এবং (10–1)’s বা 9’s কমপ্লিমেন্ট। এভাবে সকল সংখ্যা পদ্ধতির দুটি করে পূরক পদ্ধতি থাকবে r’s কমপ্লিমেন্ট এবং (r–1)’s কমপ্লিমেন্ট।
r’s কমপ্লিমেন্ট এর ধারণাঃ
যদি একটি ধণাত্বক সংখ্যা N এর ভিত্তি r এবং সংখ্যাটিতে n টি পূর্ণ সংখ্যার ডিজিট থাকে তবে সংখ্যাটির r’s কমপ্লিমেন্ট হবে rn–N, যেখানে N ≠ 0 এবং যখন N = 0 তখন r’s কমপ্লিমেন্ট = 0 । এক্ষেত্রে অবশ্যই r >1 হতে হবে, অর্থাত সংখ্যা পদ্ধতির ভিত্তি 1 অপেক্ষা বড় হলে সূত্রটি প্রযোজ্য হবে। নিচের উদাহরণসমূহ লক্ষণীয়ঃ
উদাহরণ – ১: (23450)10 এর 10’s কমপ্লিমেন্ট নির্ণয় কর।
সমাধানঃ এখানে, N = 23450, r = 10, n = 5
(23450)10 এর 10’s কমপ্লিমেন্ট = rn – N = 105 – 23450 = 76550
উদাহরণ – ২: (0.3267)10 এর 10’s কমপ্লিমেন্ট নির্ণয় কর।
সমাধানঃ এখানে, N = 0.3267, r = 10, যেহেতু পূর্ণ সংখ্যা শূণ্য তাই n = 0 (0.3267)10 এর 10’s কমপ্লিমেন্ট = rn – N = 100 – 0.3267 = 1 – 0.3267 = 0.6733
উদাহরণ – ৩: (25.639)10 এর 10’s কমপ্লিমেন্ট নির্ণয় কর।
সমাধানঃ এখানে, N = 25.639, r = 10, n = 2 (25.639)10 এর 10’s কমপ্লিমেন্ট = rn – N = 102 – 25.639 = 100 – 25.639 = 74.361
উদাহরণ – ৪: (101100)2 এর 2’s কমপ্লিমেন্ট নির্ণয় কর।
সমাধানঃ এখানে, N = 101100, r = 2, n = 6 (101100)2 এর 2’s কমপ্লিমেন্ট = rn – N = (26)10 – (101100)2 = (1000000 – 101100)2 = 010100
বাইনারী সংখ্যার জন্য কমপ্লিমেন্ট নির্ণয়ের সহজমত পদ্ধতিঃ
একটি বাইনারী সংখ্যার 1’s এবং 2’s কমপ্লিমেন্ট নির্ণয় করা যায় নিম্নোক্ত উপায়েঃ
ধাপ – ১: একটি বাইনারী সংখ্যার প্রতিটি বিটকে উল্টিয়ে দিলেই উক্ত সংখ্যাটির 1’s কমপ্লিমেন্ট পাওয়া যাবে। অর্থাত বাইনারী সংখ্যাটির প্রতিটি 1 কে 0 তে এবং প্রতিটি 0 কে 1 এ রূপান্তর করে সংখ্যাটির 1’s কমপ্লিমেন্ট পাওয়া যাবে। যেমনঃ (101100)2 এর 1’s কমপ্লিমেন্ট 010011
ধাপ – ২: প্রাপ্ত 1’s কমপ্লিমেন্ট সংখ্যার LSB বা Least Significant Bit এর সাথে একটি বাইনারী বিট 1 যোগ করলে উক্ত সংখ্যাটির 2’s কমপ্লিমেন্ট পাওয়া যায়। যেমনঃ 010011 + 000001 = 010100, অতএব, (101100)2 এর 2’s কমপ্লিমেন্ট 010100
কোড (Code) : কম্পিউটার সিস্টেমে ব্যবহৃত প্রতিটি বর্ণ, অঙ্ক, সংখ্যা, প্রতীক বা বিশেষচিহ্নকে আলাদাভাবে CPU (Central Processing Unit) কে বোঝানোর জন্যবাইনারি বিটের (০ বা ১) বিভিন্ন বিন্যাসের অদ্বিতীয় সংকেত তৈরি করা হয়।এ অদ্বিতীয় সংকেতকে বলা হয় কোড।
Encoding : বর্ণ, অঙ্ক, প্রতীক ও চিহ্নকে বাইনারিতে রূপান্তরের প্রক্রিয়া।
Decoding : বাইনারি সংখ্যাকে আবার বর্ণ, অঙ্ক, প্রতীক ও চিহ্নে রূপান্তরের প্রক্রিয়া।
প্রয়োগের ক্ষেত্রের উপর ভিত্তি করে বিভিন্ন ধরনের কোডের উদ্ভব হয়েছে।যেমন−
1. বিসিডি (BCD) কোড
2. আলফানিউমেরিক কোড (Alphanumeric code)
3. ইবিসিডিক (EBCDIC) কোড
4. অ্যাসকি (ASCII) কোড
5. ইউনিকোড (Unicode) ইত্যাদি।
BCD কোড: দশমিক সংখ্যা পদ্ধতিরপ্রতিটি অঙ্ককে ( ০ থেকে ৯ পর্যন্ত) সমতুল্য চার বিট বাইনারি দ্বারাপ্রতিস্থাপন করার পর প্রাপ্ত কোডকে BCD কোড বলে। অন্যকথায় BCDকোড একটি চার বিট বাইনারি ভিত্তিক কোড।
- পূর্ণরূপ হলো Binary Coded Decimal
- BCD was used by early computers.
- ব্যবহৃত হয় দশমিক সংখ্যাকে বাইনারি সংখ্যায় রুপান্তরের জন্য।
- এটি মূলত ৪ (চার) বিটের কোড।
- BCD কোডে বিটের সংখ্যা ৪ টি। এর মাধ্যমে ১৬ টি অদ্বিতীয় চিহ্ন নির্দেশ করা যায়।
- BCD ৮৪২১ কোড বিশেষভাবে উল্লেখযোগ্য এবং বহুল ব্যবহৃত।
- ক্যালকুলেটর, ডিজিটাল ঘড়ি, ডিজিটাল ভোল্টমিটার প্রভৃতিতে বিসিডি কোড ব্যবহৃত হয়
সুতরাং (512)10 = (010100010010)BCD
আলফানিউমেরিক কোড: অক্ষর (a-z, A-Z), অংক (0-9), এবং বিভিন্ন গাণিতিক চিহ্নসহ (+, -, =, × ইত্যাদি) আরও কতগুলো বিশেষ চিহ্নের (!, @, #, $, %, *, / ইত্যাদি) জন্য ব্যবহৃত কোডকে আলফানিউমেরিক কোড বলা হয়।
জনপ্রিয় আলফানিউমেরিক কোড হলো-
1. অ্যাসকি (ASCII) কোড
2. ইবিসিডিক (EBCDIC) কোড
3. ইউনিকোড (Unicode) ইত্যাদি।
অ্যাসকি (ASCII) কোড:
- পূর্ণরূপ American Standard Code for Inofrmation Interchange
- এর প্রকাশক আমেরিকান ন্যাশনাল স্ট্যান্ডার্ড ইন্সস্টিটিউট (ANSI)।
- ASCII দুই ধরনের হয়ে থাকে। যথা: ASCII-7 ও ASCII-8
- এটি মূলত ৭ (সাত) বা ৮ (আট) বিট আলফা নিউমেরিক কোড।
- এর মাধ্যমে ১২৮ টি (বা ২৫৬ টি) অদ্বিতীয় চিহ্ন নির্দেশ করা যায়।
- প্যারিটি বিট মূলত ভুল নির্নয়ের জন্য ব্যবহৃত হয়।
- আধুনিক কম্পিউটারে বহুল ব্যবহৃত কোড।
- মিনি ও মাইক্রোকম্পিউটারে এ কোডের বহুল প্রচলন রয়েছে।
- কম্পিউটার এবং ইনপুট/আউটপুট সরঞ্জামের মধ্যে তথ্য স্থানান্তরের জন্য এ কোড ব্যবহৃত হয়।
EBCDIC কোড:
- পূর্ণরুপ Extended Binary Coded Decimal Information Code
- আইবিএম কোম্পানি কর্তৃক উদ্ভাবিত।
- একটি ৮ বিট আলফা নিউমেরিক কোড।
- দ্বারা প্রকাশ করা যায় ২৫৬ টি অদ্বিতীয় অঙ্ক, অক্ষর এবং চিহ্ন।
- প্রাথমিকভাবে আইবিএম মেইনফ্রেম কম্পিউটারে (IBM ৩৬০ এবং ৩৭০ সিরিজের) কম্পিউটারে ব্যবহৃত হতো।
UNICODE
- পূর্ণরুপ Universal Code
- উদ্ভাবন করে যৌথভাবে (Apple+Xerox) Corporation ১৯৯১ সালে।
- ব্যবহৃত হয় বিশ্বের ছোট বড় সকল ভাষার বর্ণ ও চিহ্নকে কম্পিউটারের কোডভুক্ত করার জন্য
- The length of Unicode character is 16 bits (2 byte).
- একটি ২ বাইট বা ১৬ বিট আলফা নিউমেরিক কোড।
- এর মাধ্যমে সম্ভাব্য ৬৫,৫৩৬টি অদ্বিতীয় চিহ্নকে নির্দিষ্ট করা যায়।
- ফলে যেসব ভাষাকে কোডভুক্ত করার জন্য ৮ বিট অপর্যাপ্ত ছিল (যেমন- চায়নিজ, কোরিয়ান, জাপানিজ ইত্যাদি) সেসব ভাষার সকল চিহ্নকে সহজেই কোডভুক্ত করা সহজতর হয়েছে। বর্তমানে এ কোডের প্রচলন শুরু হয়েছে।
- বিভিন্ন উপস্থাপনায় ইউনিকোড ৮, ১৬ অথবা ৩২ বিট ক্যারেক্টার বেজ ব্যবহার করে।
- বাংলা ভাষা Unicode ভুক্ত হয়েছে Unicode consortium-এর সদস্য হয়ে।
- বুলিয়ান অ্যালজেবরাঃ যদি আমাদের চলকের মান শুধু দুইটি সংখ্যা ১ বা ০, এর মধ্যে সীমাবদ্ধথাকে তাহলে আমরা সেই অ্যালজেবরাকে বলব বুলিয়ান অ্যালজেবরা।
এখানে ১ বা ০ বলতে সাংখ্যিক মান বোঝানো হয় না। এখানে লজিকালমান সত্য আর মিথ্যা কে বোঝানো হয়। ১ দিয়ে বোঝানো হয় সত্য আর ০ দিয়ে বোঝানো হয় মিথ্যা। জর্জ বুলের নামানুসারে ঐ অ্যালজেবরার নামকরণ করা হয় বুলিয়ান অ্যালজেবরা। - বুলিয়ান অ্যালজেবরার বৈশিষ্ট্যঃ
১। বুলিয়ান অ্যালজেবরায় মাত্র দুটি অঙ্ক ‘০’ এবং ‘১’ ব্যবহৃত হয়।
২। বুলিয়ান চলকের দুটি মান থাকায় বুলিয়ান অ্যালজেবরা দশমিক অ্যালজেবরার তুলনায় অনেক সহজ পদ্ধতি।
৩। বুলিয়ান অ্যালজেবরায় কোনো ধরনের ভগ্নাংশ, লগারিদম, বর্গ, ঋণাত্মক সংখ্যা, কাল্পনিক সংখ্যা ইত্যাদি ব্যবহার করা যায় না।
৪। বুলিয়ান অ্যালজেবরায় শুধু মাত্র যোগ ও গুণের মাধ্যমে সমস্ত গাণিতিক কাজ করা যায়। ৫। বুলিয়ান অ্যালজেবরায় কোনো ধরনের জ্যামিতিক বা ত্রিকোণমিতিক সূত্র ব্যবহার করা যায় না।
বুলিয়ান চলকঃ বুলিয়ান অ্যালজেবরায় যার মান সময়ের সাথে পরিবর্তিত হয় তাকে বুলিয়ান চলক বলে। যেমন- C = A + B, এখানে A ও B হচ্ছে বুলিয়ান চলক।
বুলিয়ান ধ্রুবকঃ বুলিয়ান অ্যালজেবরায় যার মান সময়ের সাথে অপরিবর্তিত থাকে তাকে বুলিয়ান ধ্রুবক বলে। যেমন- A = 0 + 1, এখানে 0 এবং 1 হচ্ছে বুলিয়ান ধ্রুবক।
ধ্রুবকের মান সব সময় অপরিবর্তিত থাকে কিন্তু চলকের মান সময়ের সাথে সাথে পরিবর্তিত হয়। বিভিন্ন ইলেকট্রনিক বর্তনীর ইনপুট ও আউটপুটের লজিক অবস্থা নির্দিষ্ট করার জন্য বুলিয়ান চলক ও ধ্রুবক ব্যবহার করা হয়।
বুলিয়ান পূরক: বুলিয়ান অ্যালজেবরায় যেকোনো চলকের মান ০ অথবা ১ হয়। এই ০ এবং ১ কে একটি অপরটির বুলিয়ান পূরক বলা হয়। বুলিয়ান পূরকে ‘–’ বা ‘ ‘ ’ চিহ্নের মাধ্যমে প্রকাশ করা হয়। গণিতের ভাষায় লেখা হয় A এর পূরক A′।
বুলিয়ান অ্যালজেবরা তিন ধরনের মৌলিক যুক্তিমূলক ক্রিয়া সম্পাদন করে। ক্রিয়াগুলো হলো−
১। অর অপারেশন (OR Operation) বা যৌক্তিক যোগ (Logical Addition)
২। অ্যান্ড অপারেশন (AND Operation) বা যৌক্তিক গুণ (Logical Multiplication)
৩। নট অপারেশন (NOT Operation) বা যৌক্তিক উল্টানো (Logical Inversion)
বুলিয়ান স্বতঃসিদ্ধঃ বুলিয়ান অ্যালজেবরায় সমস্ত গাণিতিক কাজ করা হয় যৌক্তিক যোগ এবং যৌক্তিক গুণের সাহায্যে। বুলিয়ান অ্যালজেবরায় শুধুমাত্র যৌক্তিক যোগ ও যৌক্তিক গুণের নিয়মগুলোকে বুলিয়ান স্বতঃসিদ্ধ বলে। বুলিয়ান স্বতঃসিদ্ধ গুলোকে দু ভাগে ভাগ করা যায়। যথা:
১। যোগের বুলিয়ান স্বতঃসিদ্ধ (Boolean Postulates of OR)
২। গুণের বুলিয়ান স্বতঃসিদ্ধ (Boolean Postulates of AND)
যোগের বুলিয়ান স্বতঃসিদ্ধঃ যোগের সময় বুলিয়ান অ্যালজেবরা যেসব নিয়ম মেনে চলে তাকে যোগের বুলিয়ান স্বতঃসিদ্ধ বলে। যোগের সময় বুলিয়ান চলকগুলোর মানের মধ্যে যে যোগ চিহ্ন (+) ব্যবহার করা হয় তা প্রচলিত যোগের চিহ্ন নয়। বুলিয়ান অ্যালজেবরায় এ যোগ চিহ্নকে লজিক্যাল যোগ হিসেবে ব্যবহার করা হয়। যোগের চারটি নিয়ম প্রচলিত। যথা−
(1) 0 + 0 = 0
(2) 0 + 1 = 1
(3) 1 + 0 = 1
(4) 1 + 1 = 1
উপরের বুলিয়ান স্বতঃসিদ্ধ থেকে বলা যায় যে, বুলিয়ান অ্যালজেবরায় যোগের ক্ষেত্রে যেকোনো একটির মান ১ হলে যোগফল ১ হবে, অন্যথায় ০ হবে।
গুণের বুলিয়ান স্বতঃসিদ্ধ: গুণের সময় বুলিয়ান অ্যালজেবরা যেসব নিয়ম মেনে চলে তাকে গুণের বুলিয়ান স্বতঃসিদ্ধ বলে। গুণের সময় বুলিয়ান চলকগুলোর মানের মধ্যে গুণ চিহ্ন (.) ব্যবহার করা হয়। লজিক গুণের চারটি নিয়ম প্রচলিত। যথা:
(1) 0 . 0 = 0
(2) 0 . 1 = 0
(3) 1 . 0 = 0
(4) 1 . 1 = 1
উপরের বুলিয়ান স্বতঃসিদ্ধ থেকে বলা যায় যে, বুলিয়ান অ্যালজেবরায় গুণের ক্ষেত্রে যেকোনো একটির মান ০ হলে গুণফল ০ হবে, অন্যথায় ১ হবে।
বুলিয়ান দ্বৈতনীতি: বুলিয়ান অ্যালজেবরায় ব্যবহৃত সকল উপপাদ্য বা সমীকরণ যে দুটি নিয়ম মেনে একটি বৈধ্য সমীকরণ থেকে আর একটি বৈধ্য সমীকরণ নির্ণয় করা যায় তাকে বুলিয়ান দ্বৈতনীতি বলে। অর্থাৎ বুলিয়ান অ্যালজেবরায় অর (OR) এবং অ্যান্ড (AND) এর সাথে সম্পর্কযুক্ত সকল উপপাদ্য বা সমীকরণ দ্বৈতনীতি মেনে চলে। এ নিয়ম দু টি হলো −
১। ০ এবং ১ পরস্পর বিনিময় করে অর্থাৎ ০ এর পরিবর্তে ১ এবং ১ এর পরিবর্তে ০ ব্যবহার করে।
২। অর (+) এবং অ্যান্ড (.) পরস্পর বিনিময় করে অর্থাৎ অর (+) এর পরিবর্তে অ্যান্ড (.) এবং অ্যান্ড (.) এর পরিবর্তে অর (+) ব্যবহার করে।
উদাহরণ: ১ + ১ = ১ সমীকরণে ১ এর পরিবর্তে ০ এবং (+) এর পরিবর্তে (.) বসিয়ে পাই ০.০ = ০ এটাও একটি বৈধ্য সমীকরণ। আবার ০.১ = ০ সমীকরণে ০ এর পরিবর্তে ১ ও ১ এর পরিবর্তে ০ এবং (.) এর পরিবর্তে (+) বসিয়ে পাই ১ + ০ =১ এটাও একটি বৈধ্য সমীকরণ।
সত্যক সারণি: লজিক সার্কিটে এক বা একাধিক ইনপুটের উপর লজিক সার্কিটের আউটপুট নির্ভর করে। সুতরাং যে সারণির মাধ্যমে লজিক সার্কিটের ইনপুটের সাপেক্ষে আউটপুট প্রদর্শন করা হয়, তাকে সত্যক সারণি বলে। প্রতিটি লজিক গেইটের সত্যক সারণি ভিন্ন। যদি সত্যক সারণিতে n সংখ্যক চলক থাকে তবে ইনপুট এর অবস্থা হবে 2n সংখ্যক।
উদাহরনঃ একটি অর লজিক গেইটের ইনপুট চলক A ও B এর সাপেক্ষে আউটপুট ফাংশন F= A+B এর সত্যক সারণি দেখানো হল। যেহেতু চলক দুইটি(A ও B) তাই ইনপুট অবস্থা ২২=৪ টি হবে।
দ্বি-মানের বুলিয়ান বীজগণিতের ক্ষেত্রে স্বতঃসিদ্ধসমূহের প্রমাণ সত্যক সারণী বা Truth টেবিল-১, ২, ৩ ও ৪ এর মাধ্যমে দেখানো হলোঃ
১। উপরোক্ত টেবিল হতে দেখা যায় যে, প্রতিটি লজিক্যাল অপারেশনের ফলাফল 1 অথবা 0। যেখানে 1, 0∈B অর্থাত 1এবং 0 উভয়ে সেট B এর উপাদান সুতরাং দ্বি-মানের বুলিয়ান বীজগণিতের ক্ষেত্রে + ও . অপারেটরের সাপেক্ষে Closure প্রমাণিত।
২। উপরোক্ত টেবিল হতে দেখা যায় যে, (ক) 0+0=0, 0+1=1+0=1 এবং (খ) 1.1=1, 1.0=0.1=0 সুতরাং হান্টিংটনের ২ নং Postulate প্রমাণিত।
৩। বিনিময় সূত্র বাইনারী অপারেটর টেবিলের স্বাভাবিক নিয়মতান্ত্রিকতার মাধ্যমে প্রমাণিত।
৪। বিতরণ সূত্র X.(Y+Z)=(X.Y)+(X.Z) এবং X+(Y.Z)=(X+Y).(X+Z) প্রমাণের জন্য নিম্নের টেবিল-৪ প্রত্যক্ষ করি –
উপরোক্ত টেবিলের মাধ্যমে দেখা যায় X, Y এবং Z এর সম্ভাব্য সকল মানের ক্ষেত্রে সর্বদা X.(Y+Z)=(X.Y)+(X.Z) এবং X+(Y.Z)=(X+Y).(X+Z) প্রমাণিত।
৫। (ক) যখন X=0 তখন 0+0ʹ=0+1=1 আবার যখন X=1 তখন 1+1ʹ=1+0=1 সুতরাং X এর সকল মানের জন্য X+X̅=1 প্রমাণিত।
(ক) যখন X=0 তখন 0.0ʹ=0.1=0 আবার যখন X=1 তখন 1.1ʹ=1.0=0 সুতরাং X এর সকল মানের জন্য X.X̅=0 প্রমাণিত।
৬। টু-ভ্যাল্যূড বুলিয়ান বীজগণিতের ক্ষেত্রে কেবল দুটি নির্দিষ্ট উপাদান 0 এবং 1 আছে যেখানে 0≠1, সুতরাং টু-ভ্যাল্যূড বুলিয়ান বীজগণিতের ক্ষেত্রে Huntington এর ৬নং Postulate সিদ্ধ।
বুলিয়ান উপপাদ্যঃ যেসব উপপাদ্য ব্যবহার করে জর্জ বুল সকল প্রকার যুক্তিসংগত বিষয়ের গাণিতিক রুপ প্রদান করেন সেই উপপাদ্য গুলোকে বুলিয়ান উপপাদ্য বলা হয়।
মৌলিক উপপাদ্যঃ
ডি-মরগ্যানের উপপাদ্যঃ
প্রথম উপপাদ্যঃ যেকোন সংখ্যক চলকের যৌক্তিক যোগের কমপ্লিমেন্ট প্রত্যেক চলকের কমপ্লিমেন্টের যৌক্তিক গুণনের সমান।
দ্বিতীয় উপপাদ্যঃ যেকোন সংখ্যক চলকের যৌক্তিক গুণের কমপ্লিমেন্ট প্রত্যেক চলকের কমপ্লিমেন্টের যৌক্তিক যোগের সমান।
A ও B দুটি চলকের জন্য ডি-মরগ্যানের উপপাদ্য দুটি নিম্নরূপ−
A ও B দুইটি চলকের জন্য ডি-মরগ্যানের উপপাদ্যের প্রমাণঃ
A ,B ও C তিনটি চলকের জন্য ডি-মরগ্যানের উপপাদ্য দুটি নিম্নরূপ−
A ,B ও C তিনটি চলকের জন্য ডি-মরগ্যানের উপপাদ্যের প্রমাণঃ
লজিক গেইট: লজিক গেইট হলো এক ধরনের ইলেকট্রনিক বর্তনী যা এক বা একাধিক ইনপুট গ্রহণ করে এবং শুধু একটি আউটপুট প্রদান করে। লজিক গেইট বুলিয়ান অ্যালজেবরায় মৌলিক কাজগুলো বাস্তবায়নের জন্য ব্যবহার করা হয় । ICT এর মুলে রয়েছে লজিক গেট এবং লজিক গেট হচ্ছে বুলিয়ান অ্যালজেবরার ব্যবহারিক প্রয়োগ। - লজিক গেইট কোথায় ব্যবহৃত হয়?
ডিজিটাল সিস্টেমের মৌলিক উপাদান হচ্ছে লজিক গেইট। বর্তমানে প্রতিনিয়ত অসংখ্য ডিজিটাল আই সি তৈরি হচ্ছে যা বিভিন্ন ধরণের গুরুত্বপূর্ণ কাজে ব্যবহার করা হচ্ছে। এ সকল আই সির মূল উপাদান বিশ্লেষণ করলে শেষ পর্যন্ত গিয়ে পাওয়া যাবে লজিক গেইট। একটা ডিজিটাল আই সির কার্যাবলী অনেক জটিল হতে পারে কিন্তু একটি লজিক গেইটের ফাংশন খুবই সহজ। তাই সহজে ডিজিটাল সার্কিটের কার্যবলী বিশ্লেষণ, ডিজিটাল সার্কিট ডিজাইন ইত্যাদি সম্পর্কে জানার জন্য ডিজিটাল লজিক গেইট সম্পর্কে বিস্তারিত জ্ঞান অর্জন খুবই গুরুত্বপূর্ণ।
মৌলিক লজিক গেইটঃ যেসব গেইট অন্য কোনো গেইটের সাহায্য ছাড়া তৈরি করা যায় তাদেরকে মৌলিক লজিক গেইট বলা হয়।
মৌলিক লজিক গেইট তিনটি। যথা-
১। অর গেইট (OR Gate)
২। অ্যান্ড গেইট (AND Gate)
৩। নট গেইট (NOT Gate)
অর গেইট (OR Gate): অর গেইট হচ্ছে যৌক্তিক যোগের গেইট।অর গেইটের দুই বা ততোধিক ইনপুট থাকে এবং একটিমাত্র আউটপুট থাকে। এ গেইটের ক্ষেত্রে যেকোনো একটি ইনপুটের মান ১ হলে আউটপুট ১ হবে। অন্যথায় ০ হবে।
অর গেইটের বীজগণিতীয় ফাংশন হলো Y = A + B । যেখানে A ও B হলো OR গেইটের ইনপুট।
অ্যান্ড গেইট (AND Gate): অ্যান্ড গেইট হচ্ছে যৌক্তিক গুণের গেইট।অ্যান্ড গেইটের ক্ষেত্রে দুই বা ততোধিক ইনপুট থাকে এবং একটি মাত্র আউটপুট থাকে। এ গেইটের ক্ষেত্রে যেকোনো একটি ইনপুটের মান ০ হলে আউটপুট ০ হবে। অন্যথায় ১ হবে।
নট গেইট (NOT Gate): বুলিয়ান অ্যালজেবরায় নট অপারেশন বাস্তবায়নের জন্য নট গেইট ব্যবহৃত হয়। এ গেইটে একটি মাত্র ইনপুট এবং একটি মাত্র আউটপুট থাকে। আউটপুট হবে ইনপুটের বিপরীত। অর্থাৎ ইনপুট সংকেত ১ হলে আউটপুট সংকেত ০ হবে অথবা ইনপুট সংকেত ০ হলে আউটপুট সংকেত ১ হবে ।
যৌগিক গেইট: মৌলিক গেইটের সমন্বয়ে গঠিত লজিক গেইটকে যৌগিক গেইট বলে।
যৌগিক গেইট চার প্রকার। যথা-
১. ন্যান্ড গেইট (NAND Gate): AND গেইটের ও NOT গেইটের সমন্বয়ে তৈরি।
২. নর গেইট (NOR Gate): OR গেইটের ও NOT গেইটের সমন্বয়ে তৈরি।
৩. এক্স-অর গেইট (X-OR Gate): অর, এন্ড কিংবা নট গেইট দিয়ে এ গেইট তৈরি করা যায়।
৪. এক্স-নর গেইট (X- NOR Gate): এক্স-অর গেইটের সাথে NOT গেইট মিলিয়ে তৈরি হয়।
সার্বজনীন লজিক গেইট : যে গেইটের মাধ্যমে মৌলিক গেইটসহ অন্যান্য সকল প্রকার গেইট এর ফাংশন বাস্তবায়ন করা যায়, সেই গেইটকে সার্বজনীন গেইট বলা হয়। মৌলিক গেইট দ্বারা যেরূপ অন্যান্য সকল প্রকার গেইট তৈরি বা বাস্তবায়ন করা যায়, সেইভাবে NAND ও NOR Gate দিয়েও মৌলিক গেইট তিনটির ফাংশন বাস্তবায়ন সম্ভব। তাই NAND ও NOR Gate দুটিকে Universal Gate বা সার্বজনীন লজিক গেইট বলা হয়।
ইউনিভার্সাল গেট ব্যবহার করে মৌলিক গেটসমূহ সম্পাদনঃ
NAND গেট ব্যবহার করে নিচের চিত্রে OR, AND এবং NOT এই তিনটি মৌলিক গেট বাস্তবায়ন দেখানো হলোঃ
NOR গেট ব্যবহার করে নিচের চিত্রে OR, AND এবং NOT এই তিনটি মৌলিক গেট বাস্তবায়ন দেখানো হলোঃ
- কম্বিন্যাশন্যাল লজিক সার্কিট(COMBINATIONAL LOGIC CIRCUIT)
যে সমস্ত লজিক সার্কিট -এ কোন Memory থাকে না এবং আউটপুট কেবল ইনপুট এর উপর নির্ভর করে , তাকে কম্বিন্যাশন্যাল লজিক সার্কিট বলে। উদাহারনস্বরুপ- অ্যাডার (Adder) , সাবস্ট্রাকটার (), মালটিপ্লেক্সার (Multiplexer), ডিমাল্টিপ্লেক্সার(Demultiplexer), এনকোডার(Encoder), ডিকোডার(Decoder).
এনকোডার: এনকোডার এক ধরনের ডিজিটাল বর্তনী যার কাজ হলো মানুষের ভাষাকে কম্পিউটারের বোধগম্য যান্ত্রিক ভাষায় রূপান্তরিত করা। এ বর্তনীর সর্বাধিক 2n টি ইনপুট থেকে n টি আউটপুট লাইন পাওয়া যায়। যেকোনো মুহূর্তে একটি মাত্র ইনপুট ১ এবং বাকি সব ইনপুট ০ থাকে । এনকোডার সাধারণত ইনপুট ডিভাইস অর্থাৎ কী-বোর্ডের সাথে যুক্ত থাকে।
চিত্র: 8-to-3 এনকোডারের ব্লক চিত্র।১। এনকোডার আলফানিউমেরিক কোডকে ASCII ও EBCDIC কোডে রূপান্তর করে।
২। দশমিক সংখ্যাকে বিভিন্ন কোডে রূপান্তর করে।
৩। এনকোডারের সাহায্যে দশমিক সংখ্যাকে সমতুল্য বাইনারি সংখ্যায় রূপান্তর করে।
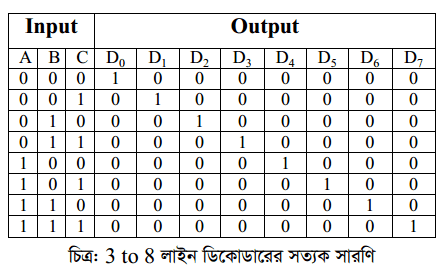
ডিকোডারঃ ডিকোডার হলো এমন একটি সমবায় সার্কিট যার কাজ হলো কম্পিউটারের বোধগম্য যান্ত্রিক ভাষাকে মানুষের ভাষায় রূপান্তরিত করা। যার সাহায্যে n টি ইনপুট থেকে সর্বাধিক 2n টি আউটপুট লাইন পাওয়া যায়। যে কোনো একটি আউটপুট লাইনের মান ১ হলে বাকি সবকটি আউটপুট লাইনের মান ০ হবে। কখন কোনো আউটপুট লাইনের মান ১ হবে তা নির্ভর করে ইনপুটগুলোর মানের উপর।চিত্র: 3-to-8 ডিকোডারের ব্লক চিত্র। 3-to-8 ডিকোডারের সত্যক সারণিঃ
ডিকোডারের ব্যবহার:
১। কম্পিউটারে ব্যবহৃত ভাষাকে মানুষের বোধগম্য ভাষায় রূপান্তর করে।
২। জটিল কোডকে সহজ কোডে রূপান্তর করে।
৩। ডিকোডার ব্যবহৃত হয় ডিসপ্লে ইউনিটে।
৪। ডিকোডারের সাহায্যে বাইনারি সংখ্যাকে সমতুল্য দশমিক সংখ্যায় রূপান্তর করা হয়।
অ্যাডার: যে সমবায় সার্কিট দ্বারা যোগ করা যায় তাকে অ্যাডার বলে। কম্পিউটারের সকল গাণিতিক কাজ বাইনারি যোগের মাধ্যমে সম্পন্ন হয়। গুণ হলো বার বার যোগ করা এবং ভাগ হলো বার বার বিয়োগ করা। আবার পূরক পদ্ধতিতে বাইনারি যোগের মাধ্যমেই বিয়োগ করা যায়। কাজেই যোগ করতে পারার মানেই হলো গুণ, বিয়োগ এবং ভাগ করতে পারা। ডিজিটাল ইলেক্ট্রনিক্সে দু ধরনের অ্যাডার আছে। যথা:
১। হাফ-অ্যাডার বা অর্ধযোগের বর্তনী(Half Adder)
২। ফুল-অ্যাডার বা পূর্ণ যোগের বর্তনী(Full Adder)
হাফ অ্যাডার (Half Adder) :
যে লজিক সার্কিট এর সাহায্যে দুটি বাইনারি বিট যোগ করা হয় তাকে হাফ অ্যাডার বলে ।দুটি বাইনারি বিট -এর লজিক্যাল যোগ হওয়ার ফলে দুটি আউটপুট তৈরি হয় একটি সাম(Sum) ও অপরটি ক্যারি(Carry)। নিম্নে ট্রুথ টেবিল সহযোগে সার্কিট অংকন করা হল ।
ট্রুথ টেবিল অনুযায়ী লিখতে পারি C= A.B এবং S = X'Y + XY' = X xor Y । C ও S সমীকরণ অনুযায়ী নিম্নে লজিক সার্কিট টি আংকন করা হল ।
ফুল অ্যাডার (Full Adder) : যে লজিক সার্কিট এর সাহায্যে তিনটি বাইনারি বিট যোগ করা হয় তাকে ফুল অ্যাডার(Full Adder) বলে । তিনটি বাইনারি বিট -এর লজিক্যাল যোগ হওয়ার ফলে দুটি আউটপুট তৈরি হয় একটি সাম(Sum) ও অপরটি ক্যারি(Carry)। নিম্নে ট্রুথ টেবিল সহযোগে সার্কিট অংকন করা হল ।
ট্রুথ টেবিল অনুযায়ী লিখতে পারি
C= X'yz + xy'z + xyz' + xyz
= z(X'y + xy') + xy(z' + z)
= z(x xor y) +xy [as z+z'=1]
= xy + z(x xor y)
S= X'y'z + x'yz' + xy'z' + xyz
= x'(y'z + yz') + x(y'z' + yz)
= x'(y xor z) + x(y xnor z) [As y'z + yz'= x xor y &y'z' + yz =x xnor y]
= x xor y xor z
C ও S সমীকরণ অনুযায়ী নিম্নে লজিক সার্কিট টি আংকন করা হল ।


















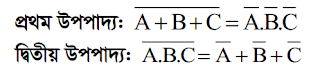
































কোন মন্তব্য নেই