Number system and digital device

সংখ্যা আবিষ্কারের ইতিহাসঃ সভ্যতার সূচনালগ্ন থেকেই মানুষ হিসাব-নিকাশের প্রয়োজনীয়তা অনুভব করে। তখন গণনার জন্য নানা রকম উপকরণ যেমন- হাতের আঙ্গুল, নুডি পাথর, কাঠি, ঝিনুক, রশির গিট, দেয়ালে দাগ কাটা ইত্যাদি ব্যবহার করা হতো। সময়ের বিবর্তনে গণনার ক্ষেত্রে বিভিন্ন চিহ্ন ও প্রতীক ব্যবহার শুরু হতে থাকে। খ্রিস্টপূর্ব ৩৪০০ সালে হায়ারোগ্লিফিক্স সংখ্যা পদ্ধতির মাধ্যমে সর্বপ্রথম গণনার ক্ষেত্রে লিখিত সংখ্যা বা চিহ্নের ব্যবহার শুরু হয়। পরবর্তিতে পর্যায়ক্রমে মেয়ান,  রোমান ও দশমিক সংখ্যা পদ্ধতির ব্যবহার শুরু হয়।

সংখ্যাঃ সংখ্যা হচ্ছে এমন একটি উপাদান যা কোনকিছু গণনা, পরিমাণ এবং পরিমাপ করার জন্য ব্যবহৃত হয়। যেমন- একাদশ শ্রেণীতে ২৪৩ জন ছাত্র আছে; এখানে ২৪৩ একটি সংখ্যা।

অংকঃ সংখ্যা তৈরির ক্ষুদ্রতম প্রতীকই হচ্ছে অংক। সকল অংক সংখ্যা কিন্তু সকল সংখ্যা অংক নয়। যেমন ২৪৩ তিন অংক বিশিষ্ট একটি সংখ্যা ,যা ২, ৪ এবং ৩ পৃথক তিনটি অংক নিয়ে গঠিত। যারা প্রত্যেকেই পৃথকভাবে একেকটি সংখ্যা।

সংখ্যা পদ্ধতিঃ কোনো সংখ্যাকে লিখা বা প্রকাশ ও এর সাহায্যে গাণিতিক হিসাব-নিকাশের জন্য ব্যবহৃত পদ্ধতিই হলো সংখ্যা পদ্ধতি। সংখ্যা পদ্ধতিতে নিমোক্ত উপাদানগুলো থাকে। যেমন-

• কতোগুলো প্রতীক। যেমন- ০,১,২,৩ …
• কতোগুলো অপারেটর। যেমন- +, -, ×, ÷ ইত্যাদি।
• কতোগুলো নিয়মাবলী। যেমন- যোগ, বিয়োগ, গুণ, ভাগ ইত্যাদির নিয়ম।

সংখ্যা পদ্ধতির প্রকারভেদঃ

অবস্থানের উপর ভিত্তি করে বা শুরু থেকে আজ পর্যন্ত সৃষ্ট সংখ্যা পদ্ধতিকে প্রধানত দুইভাগে ভাগ করা হয়। যথা:

• ১। নন-পজিশনাল (অস্থানিক) সংখ্যা পদ্ধতি
• ২। পজিশনাল (স্থানিক) সংখ্যা পদ্ধতি

নন-পজিশনাল সংখ্যা পদ্ধতিঃ যে সংখ্যা পদ্ধতিতে সংখ্যার মান সংখ্যায় ব্যবহৃত অংকসমূহের অবস্থানের উপর নির্ভর করে না তাকে নন-পজিশনাল সংখ্যা পদ্ধতি বলে। এই পদ্ধতিতে বিভিন্ন চিহ্ন বা প্রতীকের মাধ্যমে হিসাব-নিকাশের কাজ করা হতো । এই পদ্ধতিতে ব্যবহৃত প্রতীক বা অংকগুলোর পজিশন বা অবস্থান গুরত্ব পায় না। ফলে অংকগুলোর কোনো স্থানীয় মান থাকে না। শুধু অংকটির নিজস্ব মানের উপর ভিত্তি করে হিসাব-নিকাশ কার হয়। প্রাচীন কালে ব্যবহৃত হায়ারোগ্লিফিক্স (Hieroglyphics), মেয়ান ও রোমান, ট্যালি সংখ্যা পদ্ধতি নন-পজিশনাল সংখ্যা পদ্ধতির উদাহরণ।

চিত্রঃ হায়ারোগ্লিফিক্স সংখ্যা পদ্ধতির চিহ্নসমূহ  

 

পজিশনাল সংখ্যা পদ্ধতিঃ যে সংখ্যা পদ্ধতিতে সংখ্যার মান সংখ্যায় ব্যবহৃত অংকসমূহের পজিশন বা অবস্থানের উপর নির্ভর করে তাকে পজিশনাল সংখ্যা পদ্ধতি  বলে। এই সংখ্যা পদ্ধতিতে সংখ্যায় ব্যবহৃত অংকসমূহের নিজস্ব মান, স্থানীয় মান এবং সংখ্যা পদ্ধতির ভিত্তির সাহায্যে সংখ্যার মান নির্ণয় করা হয়। এই সংখ্যা পদ্ধতিতে Radix point(.) দিয়ে প্রতিটি সংখ্যাকে পূর্ণাংশ এবং ভগ্নাংশ এই দুইভাগে বিভক্ত করা হয়। যেমনঃ (১২৬.৩৪)১০   

কোন সংখ্যা পদ্ধতিতে একটি সংখ্যায় কোন অঙ্কের স্থানীয় মান হল (সংখ্যাটির বেজ) অঙ্কের পজিশন। পজিশনাল সংখ্যা পদ্ধতিতে কোন সংখ্যার পূর্নাংশের অংকগুলোর পজিশন শুরু হয় ০ থেকে(ডান থেকে বাম দিকে) এবং ভগ্নাংশের অংকগুলোর পজিশন শুরু হয় -১ থেকে(বাম থেকে ডান দিকে)।  যেমন (১২৬.৩৪)১০ সংখ্যাটির ২ অঙ্কটির স্থানীয় মান হল (১০)১= ১০ এবং ১ অঙ্কটির স্থানীয় মান হল (১০)২= ১০০।

পজিশনাল সংখ্যা পদ্ধতিতে একটি সংখ্যার বিভিন্ন অংশ:

পজিশনাল সংখ্যা পদ্ধতির প্রকারভেদ: 

 পজিশনাল সংখ্যা পদ্ধতি চার প্রকার। যথা-

• বাইনারি
• অক্টাল
• ডেসিমেল
• হেক্সাডেসিমেল

বাইনারি সংখ্যা পদ্ধতিঃ Bi শব্দের অর্থ হলো ২ (দুই)। যে সংখ্যা পদ্ধতিতে ০  ও ১ এই দুইটি প্রতিক বা চিহ্ন ব্যবহার করা হয় তাকে বাইনারি সংখ্যা পদ্ধতি বলে। যেমন-(১০১০)২। বাইনারি সংখ্যা পদ্ধতিতে যেহেতু ০ এবং ১ এই দুইটি প্রতিক বা চিহ্ন ব্যবহার করা হয় তাই এর বেজ বা ভিত্তি হচ্ছে ২। ইংল্যান্ডের গণিতবিদ জর্জ বুল বাইনারি সংখ্যা পদ্ধতি উদ্ধাবন করেন। বাইনারি সংখ্যা পদ্ধতি সবচেয়ে সরলতম সংখ্যা পদ্ধতি। বাইনারি সংখ্যা পদ্ধতির ০ এবং ১ এই দুটি মৌলিক চিহ্নকে বিট বলে এবং আট বিটের গ্রুপ নিয়ে গঠিত হয় একটি বাইট।

সকল ইলেক্ট্রনিক্স ডিভাইস শুধুমাত্র দুটি অবস্থা অর্থাৎ বিদ্যুতের উপস্থিতি এবং অনুপস্থিতি বুজতে পারে। বিদ্যুতের উপস্থিতিকে ON, HIGH, TRUE কিংবা YES বলা হয় যা লজিক লেভেল ১ নির্দেশ করে এবং বিদ্যুতের অনুপস্থিতিকে OFF, LOW, FALSE কিংবা NO বলা হয় যা লজিক লেভেল ০ নির্দেশ করে। লজিক লেভেল ০ এবং ১ বাইনারি সংখ্যা পদ্ধতির সাথে সামঞ্জন্যপূর্ণ। তাই কম্পিউটার বা সকল ইলেক্ট্রনিক্স ডিভাইসে বাইনারি সংখ্যা পদ্ধতি ব্যবহৃত হয়।

অক্টাল সংখ্যা পদ্ধতিঃ Octa শব্দের অর্থ হলো ৮ । যে সংখ্যা পদ্ধতিতে ৮টি (০,১,২,৩,৪,৫,৬,৭) প্রতিক বা চিহ্ন ব্যবহার করা হয় তাকে অকটাল সংখ্যা পদ্ধতি বলে। যেমন- (১২০)৮ । অকটাল সংখ্যা পদ্ধতিতে ০ থেকে ৭ পর্যন্ত মোট ৮ টি প্রতিক বা চিহ্ন নিয়ে যাবতীয় গাণিতিক কর্মকান্ড সম্পাদন করা হয় বলে এর বেজ বা ভিত্তি হলো ৮। অক্টাল সংখ্যা পদ্ধতিকে তিন বিট সংখ্যা পদ্ধতিও বলা হয়। কারণ অকটাল সংখ্যা পদ্ধতিতে ব্যবহৃত ০ থেকে ৭ পর্যন্ত মোট ৮ টি প্রতিক বা চিহ্নকে তিন বিটের মাধ্যমেই প্রকাশ করা যায়। ডিজিটাল সিস্টেমে বিভিন্ন ক্ষেত্রে বাইনারি সংখ্যাকে নির্ভূল ও সহজে উপস্থাপন করার জন্য অক্টাল সংখ্যা পদ্ধতি ব্যবহার করা হয়।

ডেসিমেল সংখ্যা পদ্ধতিঃ Deci শব্দের অর্থ হলো ১০। যে সংখ্যা পদ্ধতিতে ১০টি (০,১,২,৩,৪,৫,৬,৭,৮,৯) প্রতিক বা চিহ্ন ব্যবহার করা হয় তাকে ডেসিমেল বা দশমিক সংখ্যা পদ্ধতি বলে।যেমন- (১২০)১০ ।  দশমিক সংখ্যা পদ্ধতিতে ০ থেকে ৯ পর্যন্ত মোট ১০ টি প্রতিক বা চিহ্ন ব্যবহার করা হয় বলে এর বেজ বা ভিত্তি হচ্ছে ১০। ইউরোপে আরোবরা এই সংখ্যা পদ্ধতির প্রচলন করায় অনেকে এটিকে আরবি সংখ্যা পদ্ধতি নামেও অভিহিত করেন। মানুষ সাধারণত গণনার কাজে ডেসিমেল সংখ্যা পদ্ধতি ব্যবহার করে।

হেক্সাডেসিমেল সংখ্যা পদ্ধতিঃ হেক্সাডেসিমেল শব্দটির দুটি অংশ। একটি হলো হেক্সা(Hexa) অর্থাৎ ৬ এবং অপরটি ডেসিমেল অর্থাৎ ১০ , দুটো মিলে হলো ষোল। যে সংখ্যা পদ্ধতিতে ১৬ টি (০,১,২,৩,৪,৫,৬,৭,৮,৯,A,B,C,D,E,F) প্রতিক বা চিহ্ন ব্যবহার করা হয় তাকে হেক্সাডেসিমেল সংখ্যা পদ্ধতি বলে। যেমন- (১২০৯A)১৬। হেক্সাডেসিমেল সংখ্যা পদ্ধতিতে মোট ১৬ টি প্রতিক বা চিহ্ন ব্যবহার করা হয় বলে এর বেজ বা ভিত্তি হচ্ছে ১৬। হেক্সাডেসিমেল সংখ্যা পদ্ধতিকে চার বিট সংখ্যা পদ্ধতিও বলা হয়। কারণ হেক্সাডেসিমেল সংখ্যা পদ্ধতিতে ব্যবহৃত ১৬ টি (০,১,২,৩,৪,৫,৬,৭,৮,৯,A,B,C,D,E,F) প্রতিক বা চিহ্নকে চার বিটের মাধ্যমেই প্রকাশ করা যায়।  ডিজিটাল সিস্টেমে বিভিন্ন ক্ষেত্রে বাইনারি সংখ্যাকে নির্ভূল ও সহজে উপস্থাপন করার জন্য হেক্সাডেসিমেল সংখ্যা পদ্ধতি ব্যবহার করা হয়। এছাড়া বিভিন্ন মেমোরি অ্যাড্রেস ও রং এর কোড হিসেবে হেক্সাডেসিমেল সংখ্যা পদ্ধতি ব্যবহার করা হয়।

সংখ্যা পদ্ধতির বেজ (Base) বা ভিত্তিঃ কোনো একটি সংখ্যা পদ্ধতিতে ব্যবহৃত মৌলিক চিহ্নসমূহের মোট সংখ্যা বা সমষ্টিকে ঐ সংখ্যা পদ্ধতির বেজ (Base) বা ভিত্তি বলে। কোন একটি সংখ্যা কোন সংখ্যা পদ্ধতিতে লেখা তা বুঝানোর জন্য সংখ্যার সাথে বেজ বা ভিত্তিকে সাবস্ক্রিপ্ট (সংখ্যার ডানে একটু নিচে) হিসেবে লিখে প্রকাশ করা হয়। যেমন-

• বাইনারি ১০১০ কে (১০১০)২
• অক্টাল ১২০ কে (১২০)৮
• ডেসিম্যাল ১২০ কে (১২০)১০
• হেক্সাডেসিম্যাল ১২০ কে (১২০)১৬

এক নজরে বিভিন্ন পজিশনাল সংখ্যা পদ্ধতিঃ

সংখ্যা পদ্ধতিসমূহের মধ্যে পারস্পারিক রূপান্তর

চারটি সংখ্যা পদ্ধতির মধ্যে পারস্পারিক রূপান্তর করলে মোট ১২ টি রূপান্তর পাই।

একই নিয়মের রূপান্তর গুলোকে নিমোক্ত ভাবে ভাগ করা যায়।

ডেসিমেল সংখ্যাকে অন্যান্য সংখ্যা পদ্ধতিতে রূপান্তর

• ডেসিমেল সংখ্যাকে বাইনারি সংখ্যায় রূপান্তর
• ডেসিমেল সংখ্যাকে অক্টাল সংখ্যায় রূপান্তর
• ডেসিমেল সংখ্যাকে হেক্সাডেসিমেল সংখ্যায় রূপান্তর

অন্যান্য সংখ্যা পদ্ধতি থেকে ডেসিমেলে রূপান্তর

• বাইনারি সংখ্যাকে ডেসিমেল সংখ্যায় রূপান্তর 
• অক্টাল সংখ্যাকে ডেসিমেল সংখ্যায় রূপান্তর 
• হেক্সাডেসিমেল সংখ্যাকে ডেসিমেল সংখ্যায় রূপান্তর 

বাইনারি, অক্টাল ও হেক্সাডেসিমেল অথবা নন-ডেসিমেল সংখ্যা পদ্ধতিসমূহের মধ্যে পারস্পারিক রূপান্তর

• অক্টাল ও হেক্সাডেসিমেল সংখ্যাকে বাইনারি সংখ্যায় রূপান্তর
• বাইনারি সংখ্যাকে অক্টাল ও হেক্সাডেসিমেল সংখ্যায় রূপান্তর
• অক্টাল ও হেক্সাডেসিমেল সংখ্যার মধ্যে পারস্পারিক রূপান্তর

প্রথম ও দ্বিতীয় গ্রুপের রূপান্তর এর সাহায্যে এই গ্রুপের রুপান্তর দুই ধাপে নিমোক্ত চিত্রের মত করে সম্পন্ন করা যায়-

উপরের পদ্ধতি ছাড়াও নিমোক্ত উপায়েও করা যায়-

 

ডেসিমেল সংখ্যাকে অন্যান্য সংখ্যা পদ্ধতিতে রূপান্তর

পূর্ণ সংখ্যার ক্ষেত্রে-

• ধাপ-১ঃ সংখ্যাটিকে টার্গেট সংখ্যা পদ্ধতির বেজ(২/৮/১৬) দিয়ে ভাগ করতে হবে।
• ধাপ-২ঃ ধাপ-১ ভাগফলকে নিচে এবং ভাগশেষকে ডানে লিখতে হবে।
• ধাপ-৩ঃ ধাপ-১ এর ভাগফলকে পুনরায় টার্গেট সংখ্যা পদ্ধতির বেজ(২/৮/১৬) দিয়ে ভাগ করতে হবে।
• ধাপ-৪ঃ ধাপ-৩ এর ভাগফলকে নিচে ও ভাগশেষকে ডানে লিখতে হবে।

এই প্রক্রিয়া ততক্ষণ চলবে যতক্ষণ না ভাগফল শুন্য (0) হয়।

অতঃপর ভাগশেষ গুলিকে নিচ থেকে উপরের দিকে পর্যায়ক্রমে সাজিয়ে লিখলে ডেসিমেল পূর্ণসংখ্যাটির সমতুল্য বাইনারি মান পাওয়া যাবে।

 

ভগ্নাংশের ক্ষেত্রে-

• ধাপ-১ঃ ভগ্নাংশটিকে টার্গেট সংখ্যা পদ্ধতির বেজ(২/৮/১৬) দিয়ে গুণ করতে হবে।
• ধাপ-২ঃ গুণ করার পর প্রাপ্ত গুনফলের যে পূর্ণ অংশটি থাকবে সেটিকে সংরক্ষণ করতে হবে। (পূর্ণ সংখ্যা না থাকলে 0 রাখতে হবে)।
• ধাপ-৩ঃ ধাপ-১ এর গুনফলের ভগ্নাংশটিকে পুনরায় টার্গেট সংখ্যা পদ্ধতির বেজ(২/৮/১৬) দিয়ে গুণ করতে হবে।
• ধাপ-৪ঃ গুণ করার পর ধাপ-৩ এর প্রাপ্ত গুনফলের যে পূর্ণ অংশটি থাকবে সেটিকে সংরক্ষণ করতে হবে। (পূর্ণ সংখ্যা না থাকলে 0 রাখতে হবে)।

এই প্রক্রিয়া ততক্ষণ চলবে যতক্ষণ না গুনফলের ভগ্নাংশটি শুন্য (0)  হয়।

[নোটঃ প্রক্রিয়া ৩ থেকে ৪ বার চালানোর পরও যদি ভগ্নাংশটি শুন্য (0) না হয় তাহলে সেটিকে আসন্ন মান হিসেবে  ধরে নিতে হবে ]

অতঃপর সংরক্ষিত পুর্ণাংশগুলিকে উপর থেকে নিচের দিকে পর্যায়ক্রমে সাজিয়ে লিখলে ডেসিমেল ভগ্নাংশটির সমতুল্য বাইনারি মান পাওয়া যাবে।

 

ডেসিমেল সংখ্যাকে বাইনারি সংখ্যায় রূপান্তরঃ

উদাহরণঃ (17)10 কে বাইনারিতে রূপান্তর।

সুতরাং (17)10  = (10001)2

 

উদাহরণঃ (0.125)10  কে বাইনারিতে রূপান্তর।

সুতরাং (0.125)10  = (.001)2

• (35.75)10 কে বাইনারি সংখ্যা পদ্ধতিতে রূপান্তর কর। 
• (75.69)10 কে বাইনারি সংখ্যা পদ্ধতিতে রূপান্তর কর। 

ডেসিমেল সংখ্যাকে অক্টাল সংখ্যায় রূপান্তরঃ

উদাহরণঃ (423)10 কে অক্টালে রূপান্তর।

সুতরাং (423)10 = (647)8

 

উদাহরণঃ (.150)10 কে অক্টালে রূপান্তর।

সুতরাং (.150)10 = (.11463…..)8

• (75.615)10 কে অক্টাল সংখ্যা পদ্ধতিতে রূপান্তর কর। 
• (755.150)10 কে অক্টাল সংখ্যা পদ্ধতিতে রূপান্তর কর। 

ডেসিমেল সংখ্যাকে হেক্সাডেসিমেল  সংখ্যায় রূপান্তরঃ

উদাহরণঃ (423)10 কে হেক্সাডেসিমেলে রূপান্তর।  

সুতরাং (423)10 = (1A7)16

 

উদাহরণঃ (.150)10 কে হেক্সাডেসিমেলে রূপান্তর। 

সুতরাং (.150)10 = (.266…..)16  

• (615.625)10 কে হেক্সাডেসিমেল সংখ্যা পদ্ধতিতে রূপান্তর কর। 
• (125.150)10 কে হেক্সাডেসিমেল সংখ্যা পদ্ধতিতে রূপান্তর কর। 

এক নজরে দেখে নেইঃ

ডেসিমেল থেকে বাইনারিতে রূপান্তরের ক্ষেত্রে পূর্ণ সংখ্যাকে ২ দ্বারা ভাগ এবং ভগ্নাংশকে ২ দ্বারা গুণ

ডেসিমেল থেকে অক্টালে রূপান্তরের ক্ষেত্রে পূর্ণ সংখ্যাকে ৮ দ্বারা ভাগ এবং ভগ্নাংশকে ৮ দ্বারা গুণ

ডেসিমেল থেকে হেক্সাডেসিমেলে রূপান্তরের ক্ষেত্রে পূর্ণ সংখ্যাকে ১৬ দ্বারা ভাগ এবং ভগ্নাংশকে ১৬ দ্বারা গুণ

ভাগফল ০ না হওয়া পর্যন্ত ভাগের প্রক্রিয়া চলতে থাকবে।

গুনফলের ভগ্নাংশ ০ না হওয়া পর্যন্ত গুণের প্রক্রিয়া চলতে থাকবে। এক্ষেত্রে গুণের প্রক্রিয়া ৩ থেকে ৪ বার চালানোর পরও যদি ভগ্নাংশটি শুন্য (0) না হয় তাহলে সেটিকে আসন্ন মান হিসেবে ধরে নিতে হবে।

[ রপান্তরের ক্ষেত্রে ডেসিমেলের ভিত্তি ব্যবহৃত হয় না ]

যেকোন সংখ্যা পদ্ধতি থেকে ডেসিমেল বা দশমিক সংখ্যা পদ্ধতিতে রূপান্তরঃ 

পূর্ণ সংখ্যা এবং ভগ্নাংশের ক্ষেত্রে একই নিয়ম-

ধাপ-১ঃ প্রদত্ত সংখ্যার প্রতিটি অংক বা ডিজিটকে তার স্থানীয় মান দ্বারা গুণ করতে হবে।

কোন ডিজিটের স্থানীয় মান = (সংখ্যাটির বেজ) ডিজিট পজিশন

[ পূর্ন সংখ্যার ক্ষেত্রে ডিজিট পজিশন শুরু হয় ০ থেকে (ডান থেকে বাম দিকে) এবং ভগ্নাংশের ক্ষেত্রে ডিজিট পজিশন শুরু হয় -১ থেকে (বাম থেকে ডান দিকে) ] 

ধাপ-২ঃ অতঃপর গুণফলগুলোর যোগফল নির্ণয় করতে হবে।

প্রদত্ত যোগফলই হবে প্রদত্ত সংখ্যাটির সমতুল্য ডেসিমেল মান।

 

গাণিতিক ভাবে নিম্নরুপে লিখা যায়-

দশমিক সমমান = ∑ ডিজিট ×(সংখ্যাটির বেজ)ডিজিট পজিশন 

বাইনারি সংখ্যাকে ডেসিমেল সংখ্যায় রূপান্তরঃ

উদাহরণঃ (110101)2 সংখ্যাকে ডেসিমেল সংখ্যায় রূপান্তর।

সুতরাং (110101)2  = (53)10 

 

উদাহরণঃ (.1010)2 সংখ্যাকে ডেসিমেল সংখ্যায় রূপান্তর।

সুতরাং (.1010)2  = (.625)10

• (101010.0101)2 কে ডেসিমেল সংখ্যা পদ্ধতিতে রূপান্তর কর। 
• (1100011.10101)2  কে ডেসিমেল সংখ্যা পদ্ধতিতে রূপান্তর কর। 

অক্টাল সংখ্যাকে ডেসিমেল সংখ্যায় রূপান্তরঃ 

উদাহরণঃ (375)8 সংখ্যাকে ডেসিমেল সংখ্যায় রূপান্তর।

সুতরাং (375)8  = (253)10

 

উদাহরণঃ (.125)8 সংখ্যাকে ডেসিমেল সংখ্যায় রূপান্তর।

সুতরাং (.125)8  = (.166)10

• (567.247)8 কে ডেসিমেল সংখ্যা পদ্ধতিতে রূপান্তর কর। 
• (3702.6040)8  কে ডেসিমেল সংখ্যা পদ্ধতিতে রূপান্তর কর। 

হেক্সাডেসিমেল সংখ্যাকে ডেসিমেল সংখ্যায় রূপান্তরঃ  

উদাহরণঃ (3FC)16 সংখ্যাকে ডেসিমেল সংখ্যায় রূপান্তর।

সুতরাং (3FC)16  = (1020)10

 

উদাহরণঃ (.2B)16 সংখ্যাকে ডেসিমেল সংখ্যায় রূপান্তর।

সুতরাং (.2B)16  = (.168)10

• (7A6B.9B8)16 কে ডেসিমেল সংখ্যা পদ্ধতিতে রূপান্তর কর। 
• (89A.10F)16  কে ডেসিমেল সংখ্যা পদ্ধতিতে রূপান্তর কর। 

 

নন-ডেসিমেল অর্থাৎ বাইনারি, অক্টাল ও হেক্সাডেসিমেল সংখ্যাগুলোর মধ্যে নিম্নরুপে পারস্পারিক রূপান্তর করা যায়-

ধাপ-১ঃ প্রদত্ত যেকোন সংখ্যা পদ্ধতির সংখ্যাকে প্রথমে ডেসিমেলে রূপান্তর

ধাপ-২ঃ প্রাপ্ত ডেসিমেল সংখ্যাকে টার্গেট সংখ্যা পদ্ধতিতে রূপান্তর

অর্থাৎ নন-ডেসিমেল সংখ্যাগুলোর মধ্যে পারস্পারিক রূপান্তরের ক্ষেত্রে দুটি ধাপে সকল রূপান্তর করা যায়।

এছাড়া 2n (যেখানে, n=0,1,2,3,…..) ফর্মুলা ব্যবহার করেও সরাসরি অক্টাল ও হেক্সাডেসিমেল থেকে বাইনারি এবং বাইনারি  থেকে অক্টাল ও হেক্সাডেসিমেলে রূপান্তর করা যায়।

• অক্টালের ক্ষেত্রে 4 2 1   ( 2n ; যেখানে, n=0,1,2)
• হেক্সাডেসিমেলের ক্ষেত্রে 8 4 2 1 ( 2n ; যেখানে, n=0,1,2,3)

নিয়ম অনুসরণ করে  নিচে আলোচনা করা হলো-

অক্টাল সংখ্যাকে বাইনারি সংখ্যায় রূপান্তর:

পূর্ণ সংখ্যা এবং ভগ্নাংশের ক্ষেত্রে একই নিয়ম–

ধাপ-১ঃ  অক্ট্যাল সংখ্যার প্রতিটি ডিজিটের তিন বিট বাইনারি মান লিখতে হবে। [ 4 2 1  ফর্মুলা ব্যবহার করে ]

[প্রতিটি ডিজিটের বাইনারি মান ৩-বিটের কম হলে বাম পার্শ্বে প্রয়োজনীয় সংখ্যক শুন্য বসিয়ে ৩-বিট পূর্ণ করতে হবে। প্রতিটি ডিজিটের তিন বিট লেখার কারণ, অক্টাল সংখ্যার প্রতিটি ডিজিটকে ম্যাক্সিমাম তিন বিটের মাধ্যমেই প্রকাশ করা যায় ]

ধাপ-২ঃ অবশেষে প্রাপ্ত বাইনারি মান গুলিকে পাশাপাশি সাজিয়ে লিখলে অক্ট্যাল সংখ্যাটির সমতূল্য বাইনারি সংখ্যা পাওয়া যাবে।

 

উদাহরণঃ (375.24)8 সংখ্যাকে বাইনারি সংখ্যায় রূপান্তর।  

সুতরাং (375.24)8 = (011111101.010110)2

 

• (127)8 কে বাইনারি সংখ্যা পদ্ধতিতে রূপান্তর কর। 
• (.7125)8  কে বাইনারি সংখ্যা পদ্ধতিতে রূপান্তর কর। 

হেক্সাডেসিমেল সংখ্যাকে বাইনারি সংখ্যায় রূপান্তরঃ

পূর্ণ সংখ্যা এবং ভগ্নাংশের ক্ষেত্রে একই নিয়ম–

ধাপ-১ঃ হেক্সাডেসিমেল সংখ্যার প্রতিটি ডিজিটের চার বিট বাইনারি মান লিখতে হবে। [ 8 4 2 1 ফর্মুলা ব্যবহার করে ]

[প্রতিটি ডিজিটের বাইনারি মান ৪-বিটের কম হলে বাম পার্শ্বে প্রয়োজনীয় সংখ্যক শুন্য বসিয়ে ৪-বিট পূর্ণ করতে হবে। প্রতিটি ডিজিটের চার বিট লেখার কারণ, হেক্সাডেসিমেল সংখ্যার প্রতিটি ডিজিটকে ম্যাক্সিমাম চার বিটের মাধ্যমেই প্রকাশ করা যায় ]

ধাপ-২ঃ অবশেষে প্রাপ্ত বাইনারি মান গুলিকে পাশাপাশি সাজিয়ে লিখলে হেক্সাডেসিমেল সংখ্যাটির সমতূল্য বাইনারি সংখ্যা পাওয়া যাবে।

 

উদাহরণঃ (35D.4F)16 সংখ্যাকে বাইনারি সংখ্যায় রূপান্তর। 

সুতরাং (35D.4F)16 = (001101011101.01001111)2

 

• (D218)16 কে বাইনারি সংখ্যা পদ্ধতিতে রূপান্তর কর। 
• (.1C39)16  কে বাইনারি সংখ্যা পদ্ধতিতে রূপান্তর কর। 

 

বাইনারি সংখ্যাকে অক্টাল সংখ্যায় রূপান্তরঃ

ধাপ-১ঃ পূর্ণ সংখ্যার ক্ষেত্রে সংখ্যাটির ডান থেকে বাম দিকে ৩-বিট করে গ্রুপ করে নিতে হবে এবং ভগ্নাংশের ক্ষেত্রে বাম থেকে ডান দিকে ৩-বিট করে গ্রুপ করতে হবে ।

[৩-বিটের কম হলে পূর্ণ সংখ্যার ক্ষেত্রে বাম পার্শ্বে প্রয়োজনীয় সংখ্যক শুন্য বসিয়ে ৩-বিট পূর্ণ করতে হবে এবং ভগ্নাংশের ক্ষেত্রে ডান পার্শ্বে প্রয়োজনীয় সংখ্যক শুন্য বসিয়ে ৩-বিট পূর্ণ করতে হবে ]

[পূর্নাংশের ক্ষেত্রে বাম দিকে গ্রুপ করার কারণ সর্ব বামে অতিরিক্ত শূন্য বসালে মানের কোন পরিবর্তন হয় না অনুরূপ ভাবে ভগ্নাংশের ক্ষেত্রে ডান দিকে গ্রুপ করার কারণ সর্ব ডানে অতিরিক্ত শূন্য বসালে মানের কোন পরিবর্তন হয় না ]

ধাপ-২ঃ অতপর প্রতিটি ৩-বিট গ্রুপের আলাদা ভাবে অক্টাল মান লিখতে হবে।

[ প্রতিটি বাইনারি গ্রুপে যে কয়টি ১ আছে তাদের স্থানীয় মানসমূহ যোগ করলে ঐ বাইনারি গ্রুপের সমমান অক্টাল মান পাওয়া যাবে ]

ধাপ-৩ঃ অবশেষে প্রাপ্ত অক্টাল মান গুলিকে পাশাপাশি সাজিয়ে লিখলে বাইনারি সংখ্যাটির সমতূল্য অক্টাল সংখ্যা পাওয়া যাবে।

 

উদাহরণঃ (10101011.1011011)2 সংখ্যাকে অক্টাল সংখ্যায় রূপান্তর। 

সুতরাং (10101011.1011011)2 =(253.514)8

 

• (1101001)2 কে অক্টাল সংখ্যা পদ্ধতিতে রূপান্তর কর। 
• (.1010011)2  কে অক্টাল সংখ্যা পদ্ধতিতে রূপান্তর কর।

বাইনারি সংখ্যাকে হেক্সাডেসিমেল সংখ্যায় রূপান্তরঃ 

ধাপ-১ঃ পূর্ণ সংখ্যার ক্ষেত্রে সংখ্যাটির ডান থেকে বাম দিকে ৪-বিট করে গ্রুপ করে নিতে হবে এবং ভগ্নাংশের ক্ষেত্রে বাম থেকে ডান দিকে ৪-বিট করে গ্রুপ করতে হবে ।

[৪-বিটের কম হলে পূর্ণ সংখ্যার ক্ষেত্রে বাম পার্শ্বে প্রয়োজনীয় সংখ্যক শুন্য বসিয়ে ৪-বিট পূর্ণ করতে হবে এবং ভগ্নাংশের ক্ষেত্রে ডান পার্শ্বে প্রয়োজনীয় সংখ্যক শুন্য বসিয়ে ৪-বিট পূর্ণ করতে হবে ]

[পূর্নাংশের ক্ষেত্রে বাম দিকে গ্রুপ করার কারণ সর্ব বামে অতিরিক্ত শূন্য বসালে মানের কোন পরিবর্তন হয় না অনুরূপ ভাবে ভগ্নাংশের ক্ষেত্রে ডান দিকে গ্রুপ করার কারণ সর্ব ডানে অতিরিক্ত শূন্য বসালে মানের কোন পরিবর্তন হয় না ]

ধাপ-২ঃ অতপর প্রতিটি ৪-বিট গ্রুপের আলাদা ভাবে হেক্সাডেসিমেল মান লিখতে হবে।

[ প্রতিটি বাইনারি গ্রুপে যে কয়টি ১ আছে তাদের স্থানীয় মানসমূহ যোগ করলে ঐ বাইনারি গ্রুপের সমমান হেক্সাডেসিমেল মান পাওয়া যাবে ]

ধাপ-৩ঃ অবশেষে প্রাপ্ত হেক্সাডেসিমেল মান গুলিকে পাশাপাশি সাজিয়ে লিখলে বাইনারি সংখ্যাটির সমতূল্য হেক্সাডেসিমেল সংখ্যা পাওয়া যাবে।

 

উদাহরণঃ (0111001011.1010011)2 সংখ্যাকে হেক্সাডেসিমেল সংখ্যায় রূপান্তর।

সুতরাং (0111001011.1010011)2 = (1CB.A6)16 

 

• (1101101)2 কে হেক্সাডেসিমেল  সংখ্যা পদ্ধতিতে রূপান্তর কর। 
• (.1010011)2  কে হেক্সাডেসিমেল সংখ্যা পদ্ধতিতে রূপান্তর কর।

 

অক্টাল সংখ্যাকে হেক্সাডেসিমেল সংখ্যায় রূপান্তরঃ

ধাপ-১ঃ প্রথমে অক্টাল সংখ্যাটিকে বাইনারি সংখ্যায় রুপান্তর করতে হবে

ধাপ-২ঃ  প্রাপ্ত বাইনারি সংখ্যাটিকে হেক্সাডেসিমেল সংখ্যায় রূপান্তর করতে হবে

অথবা 

ধাপ-১ঃ প্রথমে অক্টাল সংখ্যাটিকে ডেসিমেল সংখ্যায় রুপান্তর করতে হবে

ধাপ-২ঃ প্রাপ্ত ডেসিমেল সংখ্যাটিকে হেক্সাডেসিমেল সংখ্যায় রূপান্তর করতে হবে

 

উদাহরণঃ (375.246)8 সংখ্যাকে হেক্সাডেসিমেল সংখ্যায় রূপান্তর। 

 

• (5273)8 কে হেক্সাডেসিমেল সংখ্যা পদ্ধতিতে রূপান্তর কর। 
• (.5137)8  কে হেক্সাডেসিমেল সংখ্যা পদ্ধতিতে রূপান্তর কর।

হেক্সাডেসিমেল সংখ্যাকে অক্টাল সংখ্যায় রূপান্তরঃ

ধাপ-১ঃ প্রথমে হেক্সাডেসিমেল সংখ্যাটিকে বাইনারি সংখ্যায় রুপান্তর করতে হবে

ধাপ-২ঃ প্রাপ্ত বাইনারি সংখ্যাটিকে অক্টাল সংখ্যায় রূপান্তর করতে হবে

অথবা 

ধাপ-১ঃ প্রথমে হেক্সাডেসিমেল সংখ্যাটিকে ডেসিমেল সংখ্যায় রুপান্তর করতে হবে

ধাপ-২ঃ প্রাপ্ত ডেসিমেল সংখ্যাটিকে অক্টাল সংখ্যায় রূপান্তর করতে হবে

উদাহরণঃ (08B.FCD)16 সংখ্যাকে অক্টাল সংখ্যায় রূপান্তর।

 

• (5F293)16 কে অক্টাল সংখ্যা পদ্ধতিতে রূপান্তর কর। 
• (.A127)16  কে অক্টাল সংখ্যা পদ্ধতিতে রূপান্তর কর।

বিভিন্ন সংখ্যা পদ্ধতির যোগঃ

ডেসিমেল সংখ্যার যোগঃ

১। ডেসিমেল সংখ্যায় একাধিক অংকের যোগফল ভিত্তি ১০ এর সমান বা তার বেশি হলে যোগফল থেকে ভিত্তি ১০ বিয়োগ করতে হবে (এক্ষেত্রে যোগফল যতক্ষণ না ১০ এর কম হবে ততক্ষণ বিয়োগ করতে হবে)।

২। যতবার বিয়োগ করা হবে ক্যারি হবে তত।

উদাহরনঃ (5689)10 এবং (7989)10 সংখ্যা দুটির যোগ।

অক্টাল সংখ্যার যোগঃ

১। অক্টাল সংখ্যায় একাধিক অংকের যোগফল ভিত্তি ৮ এর সমান বা তার বেশি হলে যোগফল থেকে ভিত্তি ৮ বিয়োগ করতে হবে (এক্ষেত্রে যোগফল যতক্ষণ না ৮এর কম হবে ততক্ষণ বিয়োগ করতে হবে)।

২। যতবার বিয়োগ করা হবে ক্যারি হবে তত।

উদাহরনঃ (5647)8 এবং (7261)8 সংখ্যা দুটির যোগ।

হেক্সাডেসিমেল সংখ্যার যোগঃ

১। হেক্সাডেসিমেল সংখ্যায় একাধিক অংকের যোগফল ভিত্তি ১৬ এর সমান বা তার বেশি হলে যোগফল থেকে ভিত্তি ১৬ বিয়োগ করতে হবে (এক্ষেত্রে যোগফল যতক্ষণ না ১৬ এর কম হবে ততক্ষণ বিয়োগ করতে হবে)।

২। যতবার বিয়োগ করা হবে ক্যারি হবে তত।

উদাহরনঃ  (BFC3)16 এবং (AB8D)16 সংখ্যা দুটির যোগ।

বাইনারি সংখ্যার যোগঃ

১। বাইনারি সংখ্যায় একাধিক অংকের যোগফল ভিত্তি ২ এর সমান বা তার বেশি হলে যোগফল থেকে ভিত্তি ২ বিয়োগ করতে হবে (এক্ষেত্রে যোগফল যতক্ষণ না ২ এর কম হবে ততক্ষণ বিয়োগ করতে হবে)।

২। যতবার বিয়োগ করা হবে ক্যারি হবে তত।

উদাহরনঃ (1110)2 এবং (1111)2 সংখ্যা দুটির যোগ।

 

নোটঃ

 ১। ভিন্ন সংখ্যা পদ্ধতির সংখ্যার মধ্যে যোগ করার জন্য সংখ্যাগুলোকে একই পদ্ধতিতে রূপান্তর করে তারপর যোগ করতে হবে।

২। যদি কোন নির্দিস্ট সংখ্যা পদ্ধতিতে যোগ করতে বলে, তাহলে সংখ্যাগুলোকে ঐ নির্দিস্ট সংখ্যা পদ্ধতিতে রূপান্তর করে তারপর যোগ করতে হবে।

৩। যদি যোগফল কোন নির্দিস্ট সংখ্যা পদ্ধতিতে প্রকাশ করতে বলে, সেক্ষেত্রে যেকোন সংখ্যা পদ্ধতিতে যোগ করে যোগফল উল্লিখিত সংখ্যা পদ্ধতিতে রূপান্তর করলেই হবে।

৪। কোন একটি সংখ্যার পরের সংখ্যা বলতে বুঝায় ঐ সংখ্যা পদ্ধতিতে সংখ্যাটির সাথে ১ যোগ।

 

• (5B.3D)16 এবং (74.05)8 সংখ্যা দুটির যোগফল বাইনারিতে প্রকাশ কর।   
• (11001.011)2 এবং (1101.01)2 সংখ্যা দুটির যোগফল অক্টালে প্রকাশ কর।   
• (52B.5D)16 এবং (70.25)8 সংখ্যা দুটি বাইনারিতে যোগ কর।   

 

বিভিন্ন গাণিতিক সমস্যা সমাধানের ক্ষেত্রে ধনাত্মক ও ঋণাত্মক সংখ্যা ব্যবহার করা হয়। সংখ্যাটি ধনাত্মক নাকি ঋণাত্মক তা বুঝানোর জন্য সাধারণত সংখ্যার পূর্বে চিহ্ন(+ অথবা -) ব্যবহৃত হয়। অর্থাৎ যখন কোন সংখ্যার পূর্বে ধনাত্মক(+) বা ঋণাত্মক(-) চিহ্ন থাকে তখন সেই সংখ্যাকে চিহ্নযুক্ত সংখ্যা বা সাইনড নম্বর বলা হয়।

বাইনারি পদ্ধতিতে চিহ্নযুক্ত সংখ্যা উপস্থাপনের জন্য প্রকৃত মানের পূর্বে একটি অতিরিক্ত বিট যোগ করা হয়। এ অতিরিক্ত বিটকে চিহ্ন বিট বলে। চিহ্ন বিট 0 হলে সংখ্যাটি ধনাত্মক এবং চিহ্নবিট ১ হলে সংখ্যাটিকে ঋণাত্মক ধরা হয়।

চিহ্নযুক্ত সংখ্যার উপস্থাপনাঃ কম্পিউটার সিস্টেমে ঋণাত্মক(-) চিহ্ন যুক্ত সংখ্যা বা ঋণাত্মক সংখ্যা উপস্থাপনার জন্য তিনটি পদ্ধতি আছে। যথাঃ

• প্রকৃত মান গঠন (Signed magnitude form)
• ১ এর পরিপূরক গঠন (1’s Complement form)
• ২ এর পরিপূরক গঠন (2’s Complement form)

এক্ষেত্রে তিনটি পদ্ধতিতেই ধনাত্মক সংখ্যার উপস্থাপনা একই। অর্থাৎ ধনাত্মক সংখ্যার ক্ষেত্রে চিহ্ন বিট ছাড়া বাকি অংশটি সংখ্যার মান জ্ঞাপন করে। তবে ঋণাত্মক সংখ্যার ক্ষেত্রে উপস্থাপনা ভিন্ন ভিন্ন হয়।

উপরিউক্ত তিনটি পদ্ধতিতে চিহ্ন যুক্ত সংখ্যা উপস্থাপনার জন্য রেজিস্টার সম্পর্কে প্রাথমিক ধারণা থাকতে হবে। রেজিস্টার হলো একগুচ্ছ  ফ্লিপ-ফ্লপ এবং গেইটের সমন্বয়ে গঠিত সার্কিট যা অস্থায়ী মেমোরি হিসেবে কাজ করে। এর প্রত্যেকটি ফ্লিপ-ফ্লপ একটি করে বাইনারি বিট সংরক্ষণ করতে পারে। n বিটের একটি রেজিস্টার n বিটের বাইনারি তথ্য ধারণ করতে পারে। অর্থাৎ ৮-বিট রেজিস্টার, ১৬- বিট রেজিস্টার, ৩২-বিট রেজিস্টার ইত্যাদি যথাক্রমে ৮, ১৬, ৩২ বিট তথ্য ধারণ করতে পারে। এই অধ্যায়ের শেষের দিকে রেজিস্টার সম্পর্কে বিস্তারিত আলোচনা করা হয়েছে।

৮-বিট রেজিস্টারের ক্ষেত্রে সর্বডানের ৭-বিট হল ডেটা বিট এবং সর্ব বামের বিটটি চিহ্ন বিট। একইভাবে ১৬-বিট রেজিস্টারের ক্ষেত্রে সর্বডানের ১৫-বিট হল ডেটা বিট এবং সর্ব বামের বিটটি চিহ্ন বিট। অর্থাৎ n-bit রেজিস্টারের ক্ষেত্রে সর্বডানের n-1 বিট হল ডেটা বিট এবং সর্ব বামের বিটটি চিহ্ন বিট হিসেবে ব্যবহৃত হয়।

কখন কত বিট রেজিস্টার ব্যবহার করতে হবে তা নির্ভর করে প্রদত্ত সংখ্যার উপর। যদি একটি সংখ্যার ডেটা বিট ৭ বিটের বেশি হয় তখন ১৬ রেজিস্টার ব্যবহার করতে হবে এবং ডেটা বিট ১৫ বিটের বেশি হলে ৩২ রেজিস্টার ব্যবহার করতে হবে।

প্রকৃত মান গঠন (Signed magnitude form):

প্রকৃত মান গঠন প্রক্রিয়ায় কোন ধনাত্মক ও ঋণাত্মক সংখ্যা ৮-বিট রেজিস্টারে উপস্থাপনের ক্ষেত্রে রেজিস্টারের সর্বডানের ৭-বিট ডেটা বিট এবং সর্ব বামের বিটটি চিহ্ন বিট হিসেবে ব্যবহৃত হয়। এক্ষেত্রে ধনাত্মক চিহ্নের জন্য চিহ্ন বিট 0 এবং ঋণাত্মক চিহ্নের জন্য চিহ্ন বিট 1। এই প্রক্রিয়ায় +০ এবং -০ এর ভিন্ন ভিন্ন মান পাওয়া যায় যা বাস্তবের সাথে অসামঞ্জস্যপূর্ণ। প্রকৃত মান গঠন সহজ হলেও এর জন্য জটিল বর্তনীর প্রয়োজন হয়।

প্রকৃত মান গঠন প্রক্রিয়ায় +5 এবং -5  কে ৮-বিট রেজিস্টারে উপস্থাপনঃ 

এক্ষেত্রে ডেটা বিট ৭-বিটের কম হলে বাকিগুলো ০ দ্বারা পূর্ন করতে হবে।

যেহেতু ৮-বিট রেজিস্টার ব্যবহৃত হয়েছে, তাই ডেটা বিট ৭-বিট। কিন্তু ৫ এর ডেটা বিট ১০১ তিন বিট। তা বাকি গুলো ০ দ্বারা পূর্ন করা হয়েছে।

১ এর পরিপূরক গঠন (1’s Complement form):

কোন বাইনারি সংখ্যার প্রতিটি বিটকে পূরক করে বা উল্টিয়ে যে সংখ্যা পাওয়া যায় তাকে ১ এর পরিপূরক বলা হয়। এই প্রক্রিয়ায় ধনাত্মক সংখ্যার উপস্থাপন প্রকৃত মান গঠনের মতই। অর্থাৎ ধনাত্মক চিহ্নযুক্ত সংখ্যার ক্ষেত্রে ধনাত্মক চিহ্নের জন্য চিহ্ন বিট 0 এবং বাকি ৭-বিট ব্যবহৃত হয় ডেটা বিটের জন্য। ঋণাত্মক চিহ্নযুক্ত সংখ্যার মান নির্ণয়ের জন্য ধনাত্মক চিহ্নযুক্ত সংখ্যার মান নির্ণয় করতে হয়। তারপর চিহ্ন-বিট সহ সবগুলো বিটকে উল্টিয়ে(অর্থাৎ 0 থাকলে ১ এবং ১ থাকলে 0 হয়) ঋণাত্মক চিহ্নযুক্ত সংখ্যার মান নির্নয় করা হয়। এই প্রক্রিয়াতেও +০ এবং -০ এর ভিন্ন ভিন্ন মান পাওয়া যায় যা বাস্তবের সাথে অসামঞ্জস্যপূর্ণ।

১ এর পরিপূরক গঠন প্রক্রিয়ায় +5 এবং -5 কে ৮-বিট রেজিস্টারে উপস্থাপনঃ

এক্ষেত্রেও ডেটা বিট ৭-বিটের কম হলে বাকিগুলো ০ দ্বারা পূর্ন করতে হবে।

২ এর পরিপূরক গঠন (2’s Complement form):

কোন বাইনারি সংখ্যার ১ এর পরিপূরকের সাথে বাইনারি ১ যোগ করলে যে সংখ্যা পাওয়া যায় তাকে ২ এর পরিপূরক বলা হয়।এই প্রক্রিয়াতেও ধনাত্মক সংখ্যার উপস্থাপন প্রকৃত মান গঠনের মতই। অর্থাৎ ধনাত্মক চিহ্নযুক্ত সংখ্যার ক্ষেত্রে ধনাত্মক চিহ্নের জন্য চিহ্ন বিট 0 এবং বাকি ৭-বিট ব্যবহৃত হয় ডেটা বিটের জন্য। ঋণাত্মক চিহ্নযুক্ত সংখ্যার মান নির্ণয়ের জন্য  প্রথমে সংখ্যাটির ধনাত্মক সংখ্যার মান নির্ণয় করতে হয়। তারপর ধনাত্মক সংখ্যার মানের ১ এর পরিপূরক করতে হয়। শেষে ১ এর পরিপূরকে প্রাপ্ত মানের সাথে বাইনারি ১ যোগ করতে হয়। ২ এর পরিপূরক গঠনে +০ এবং -০ এর মান একই যা বাস্তবের সাথে সামঞ্জস্যপূর্ণ। এই প্রক্রিয়ার বিভিন্ন সুবিধার কারণে ডিজিটাল ডিভাইসে ব্যপকভাবে ব্যবহৃত হচ্ছে।

২ এর পরিপূরক গঠন প্রক্রিয়ায় +5 এবং -5 কে ৮-বিট রেজিস্টারে উপস্থাপনঃ

এক্ষেত্রেও ডেটা বিট ৭-বিটের কম হলে বাকিগুলো ০ দ্বারা পূর্ন করতে হবে।

 

২ এর পরিপূরক গঠনের গুরুত্বঃ

১। প্রকৃত মান গঠন ও ১ এর পরিপূরক গঠনে +০ এবং -০ এর ভিন্ন ভিন্ন মান পাওয়া যায় যা বাস্তবের সাথে অসামঞ্জস্যপূর্ণ। কিন্তু  ২ এর পরিপূরক গঠনে +০ এবং -০ এর মান একই যা বাস্তবের সাথে সামঞ্জস্যপূর্ণ।

২। ২ এর পরিপূরক গঠনে সরল বর্তনী প্রয়োজন যা দামে সস্তা এবং দ্রুত গতিতে কাজ করে।

৩। ২ এর পরিপূরক গঠনে চিহ্ন যুক্ত সংখ্যা এবং চিহ্নবিহীন সংখ্যা যোগ করার জন্য একই বর্তনী ব্যবহার করা যায়।

৪। ২ এর পরিপূরক গঠনে যোগ ও  বিয়োগের জন্য একই বর্তনী ব্যবহার করা যায়। তাই আধুনিক কম্পিউটারে ২ এর পরিপূরক গঠন ব্যবহৃত হয়।

 

২ এর পরিপূরক পদ্ধতিতে যোগঃ 

১। প্রদত্ত চিহ্নযুক্ত সংখ্যা দুটির ২ এর পরিপূরক পদ্ধতিতে মান নির্নয় করতে হবে।

২। অতঃপর প্রাপ্ত মানের বাইনারি যোগ করতে হবে।

৩। যোগফলে অতিরিক্ত ক্যারি বিট (অর্থাৎ ৮ বিট রেজিস্টারের ক্ষেত্রে যোগফল ৮ বিটের বেশি হলে সর্ব বামের বিটটিকে ক্যারি বিট বলা হয়) থাকলে তা বাদ দিতে হবে।

৪। এভাবে প্রাপ্ত সংখ্যাটিই হবে প্রদত্ত সংখ্যা দুটির যোগফল।

 

উদাহরন-১ঃ ৮-বিট রেজিস্টারের জন্য -২৫ এবং +১২ এর যোগফল নির্ণয়।  

উদাহরন-২ঃ ৮-বিট রেজিস্টারের জন্য +২৫ এবং -১২ এর যোগফল নির্ণয়।  

উদাহরন-৩ঃ ৮-বিট রেজিস্টারের জন্য -২৫ এবং -১২ এর যোগফল নির্ণয়।  

উদাহরন-৪ঃ ৮-বিট রেজিস্টারের জন্য +২৫ এবং +১২ এর যোগফল নির্ণয়। 

 

২ এর পরিপূরক পদ্ধতিতে বিয়োগঃ

১। প্রদত্ত চিহ্নযুক্ত সংখ্যা দুটির মধ্যে যে সংখ্যাটি বিয়োগ করতে হবে তার চিহ্ন পরিবর্তন করে তার ২ এর পরিপূরক পদ্ধতিতে মান নির্নয় করতে হবে(অর্থাৎ +৫ থাকলে -৫ এর মান অথবা -৫ থাকলে +৫ এর মান নির্নয় করতে হবে)।

২। অপর চিহ্নযুক্ত সংখ্যাটির ২ এর পরিপূরক পদ্ধতিতে মান নির্নয় করতে হবে।

৩। অতঃপর প্রাপ্ত মানের বাইনারি যোগ করতে হবে (বিয়োগের ক্ষেত্রেও যোগ করতে হয়)।

৪। যোগফলে অতিরিক্ত ক্যারি বিট (অর্থাৎ ৮ বিট রেজিস্টারের ক্ষেত্রে যোগফল ৮ বিটের বেশি হলে সর্ব বামের বিটটিকে ক্যারি বিট বলা হয়) থাকলে তা বাদ দিতে হবে।

৫। এভাবে প্রাপ্ত সংখ্যাটিই হবে প্রদত্ত সংখ্যা দুটির বিয়োগফল।

 

উদাহরন-১ঃ ৮-বিট রেজিস্টারের জন্য -২৫ থেকে +১২ বিয়োগ কর।  

= – ২৫ – ১২

= – ২৫ + (-১২)

উদাহরন-২ঃ ৮-বিট রেজিস্টারের জন্য +২৫ থেকে -১২ বিয়োগ কর। 

উদাহরন-৩ঃ ৮-বিট রেজিস্টারের জন্য -২৫ থেকে -১২ বিয়োগ কর। 

উদাহরন-৪ঃ ৮-বিট রেজিস্টারের জন্য +২৫ থেকে +১২ বিয়োগ কর।  

 কোড: মানুষের ভাষায় ব্যবহৃত প্রতিটি বর্ণ, অঙ্ক, সংখ্যা, প্রতীক বা বিশেষ চিহ্নকে ডিজিটাল ডিভাইসে উপস্থাপনের জন্য বাইনারি বিটের অদ্বিতীয় বিন্যাস ব্যবহৃত হয়, এই অদ্বিতীয় বিন্যাসকে বলা হয় কোড।

প্রয়োগের ক্ষেত্রের উপর ভিত্তি করে বিভিন্ন ধরনের কোডের উদ্ভব হয়েছে। যেমন−

• বিসিডি (BCD) কোড
• আলফানিউমেরিক কোড (Alphanumeric code)
  • অ্যাসকি (ASCII)
  • ইবিসিডিক (EBCDIC)
  • ইউনিকোড (Unicode)

 

BCD কোড: BCD এর পূর্ণ রূপ হলো  Binary Coded Decimal। ডেসিমেল সংখ্যার প্রতিটি অঙ্ককে (০ থেকে ৯ পর্যন্ত) সমতুল্য চার-বিট বাইনারি দ্বারা উপস্থাপন করার পর প্রাপ্ত কোডকে BCD কোড বলে। অন্যকথায় BCD কোড একটি ৪-বিট বাইনারি ভিত্তিক কোড। BCD কোড কোন সংখ্যা পদ্ধতি নয়। এটি সাধারণত ডেসিমেল সংখ্যার প্রতিটি অংককে বাইনারিতে এনকোড করার পদ্ধতি। তাই বলা যায় BCD কোড এবং বাইনারি সংখ্যা এক নয়। BCD কোড ক্যালকুলেটর, ডিজিটাল ঘড়ি ও ভোল্টমিটার প্রভৃতিতে ব্যবহৃত হয়।

নিম্নে কয়েক ধরণের BCD কোডের নাম দেওয়া হলো-

• BCD 8421 কোড (NBCD– Natural Binary Coded Decimal)
• BCD 7421 কোড
• BCD 5421 কোড
• BCD 2421 কোড
• Excess-3 কোড

0-৯ পর্যন্ত ডেসিমেল সংখ্যার বিভিন্ন BCD কোড নিচের টেবিলে দেখানো হল- 

উদাহরণ-১: (592)10  কে BCD কোডে রূপান্তর কর।

সুতরাং (592)10  = (010110010010)BCD

উদাহরণ-2:(807)10  কে BCD কোডে রূপান্তর কর।  

 

আলফানিউমেরিক কোড: কম্পিউটার সিস্টেমে সংখ্যাসূচক(০-৯) চিহ্নের পাশাপাশি বিভিন্ন বর্ণ (a-z,A-Z) ও বিভিন্ন গাণিতিক এবং বিশেষ চিহ্ন (+,$,*,#,% ইত্যাদি) ব্যবহৃত হয়। এসকল সংখ্যা, বর্ণ ও চিহ্নের জন্য যে কোড ব্যবহৃত হয় তাকে আলফানিউমেরিক কোড বলে। বিভিন্ন আলফানিউমেরিক কোড-

• ইবিসিডিক (EBCDIC)
• অ্যাসকি (ASCII)
• ইউনিকোড (Unicode)

 

ইবিসিডিআইসি কোড (EBCDIC): EBCDIC এর পূর্ণরূপ Extended Binary Coded Decimal Information Code । এটি  BCD কোডের নতুন সংস্করণ। BCD কোড ৪-বিটের কোড যার মাধ্যমে ২৪ =১৬ টি বিভিন্ন সংখ্যা কোডভুক্ত করা যেত। পরবর্তিতে BCD কোডের সাথে বামে ০-৯ সংখ্যার জন্য ১১১১, A-Z বর্ণের জন্য ১১০০,১১০১ ও ১১১০ এবং বিশেষ চিহ্নের জন্য ০১০০,০১০১,০১১০ ও ০১১১  ৪-বিটের জোন বিট যোগ করে ৮-বিটের EBCDIC কোড প্রকাশ করা হয়। ফলে এ কোড দ্বারা ২৮  অর্থাৎ ২৫৬টি  অঙ্ক, বর্ণ এবং বিশেষ চিহ্ন প্রকাশ করা যায়।

মনে করি  ৫, কে EBCDIC কোডে প্রকাশ করতে হবে। তাহলে  ৫ এর বিসিডি  ৮৪২১  কোডে মান হবে  ০১০১। সুতরাং,  ৫ এর EBCDIC কোডে মান হবে ১১১১০১০১।

IBM মেইনফ্রেম বা এর সমকক্ষ ও মিনি কম্পিউটারে EBCDIC কোড ব্যবহার করা হয়।

 

ASCII:  ASCII এর পূর্ণ নাম American Standard Code For Information Interchange । ASCII আধুনিক কম্পিউটারে বহুল ব্যবহৃত কোড। এর প্রকাশক ANSI(American National Standard Institute )। ASCII দুই ধরনের হয়ে থাকে। যথা:

• ASCII-7
• ASCII-8

ASCII-7 এ ৭টি  বিট থাকে, যার বাম দিকের তিনটি বিটকে জোন বিট এবং ডানদিকের চারটি বিটকে বলা হয় সংখ্যাসূচক বিট। ASCII-7 এ ৭ বিট দ্বারা মোট ২৭= ১২৮ টি অদ্বিতীয় চিহ্ন কম্পিউটারকে অদ্বিতীয়ভাবে বুঝানো যায়।

ASCII-7 এর সাথে বামে একটি প্যারিটি বিট যোগ করে ASCII-8 তৈরি করা হয়। ASCII-8 এর ৮ বিট দ্বারা মোট ২৮ = ২৫৬ টি অদ্বিতীয় চিহ্ন কম্পিউটারকে অদ্বিতীয়ভাবে বুঝানো যায়। বর্তমানে ASCII বলতে ASCII-8 কেই বুঝানো হয়।

বিভিন্ন ধরণের কীবোর্ড, মাউস, মনিটর, প্রিন্টার ইত্যাদি যন্ত্রের মধ্যে আলফানিউমেরিক ডেটা আদান-প্রদান করার জন্য ASCII ব্যপকভাবে ব্যবহৃত হয়।

ASCII কোড দেখতে ক্লিক করুন

 

Unicode: Unicode এর পূর্ণনাম হলো Universal Code বা সার্বজনীন কোড। ASCII এর সাহায্যে ২৫৬ টি চিহ্নকে কম্পিউটারে অদ্বিতীয়ভাবে বুঝানো যায়। ফলে ইংরেজি ভাষা ব্যতীত অন্য কোন ভাষা কম্পিউটারে ব্যবহার করা যেত না।  বিশ্বের সকল ভাষাকে কম্পিউটারে কোডভুক্ত করার জন্য বড় বড় কোম্পানিগুলো একটি মান তৈরি করেছেন যাকে ইউনিকোড বলা হয়। Apple Computer Corporation এবং Xerox Corporation এর একদল প্রকৌশলী ইউনিকোড উদ্ভাবন করেন। ইউনিকোড মূলত ২ বাইট বা ১৬ বিটের কোড। এ কোডের মাধ্যমে ২১৬  বা ৬৫,৫৩৬ টি অদ্বিতীয় চিহ্ন কম্পিউটারকে অদ্বিতীয়ভাবে বুঝানো যায়।

ইউনিকোডের সুবিধাঃ

• ইউনিকোড ২ বাইট বা ১৬ বিটের কোড ফলে ২১৬   = ৬৫৫৩৬ টি চিহ্নকে কম্পিউটার সিস্টেমে অদ্বিতীয়ভাবে বুঝানো যায়।
• এই কোডের সাহায্যে বিশ্বের ছোট বড় সকল ভাষাকে কম্পিউটারে বুঝানো যায়।
• ইউনিকোডের প্রথম ২৫৬ টি কোড অ্যাসকি কোডের অনুরুপ। তাই বলা যায় ইউনিকোড অ্যাসকি কোডের সাথে কম্প্যাটিবল।

বুলিয়ান অ্যালজেবরাঃ

বুলিয়ান অ্যালজেবরার উদ্ভাবক হলেন প্রখ্যাত ইংরেজ গণিতবিদ জর্জ বুল। জর্জ বুল সর্বপ্রথম গণিত ও যুক্তির মধ্যে সম্পর্ক আবিষ্কার করেন এবং গণিত ও যুক্তির ওপর ভিত্তি করে এক ধরণের অ্যালজেবরা তৈরি করেন, যাকে বুলিয়ান অ্যালজেবরা বলা হয়।

বুলিয়ান অ্যালজেবরা মূলত লজিকের সত্য অথবা মিথ্যা এ দুটি স্তরের উপর ভিত্তি করে তৈরি করা হয়েছে। অপরদিকে সকল ডিজিটাল ডিভাইস বাইনারি পদ্ধতিতে কাজ করে। এই ডিজিটাল ডিভাইসে গাণিতিক ও যুক্তিমূলক কাজ করার জন্য বুলিয়ান অ্যালজেবরা ব্যবহৃত হয়।

বুলিয়ান অ্যালজেবরার সত্য ও মিথ্যাকে যথাক্রমে বাইনারি  “১“ এবং “০” দ্বারা পরিবর্তন করে ডিজিটাল ডিভাইসের সকল গাণিতিক সমস্যা বুলিয়ান অ্যালজেবরার সাহায্যে সমাধান সম্ভব হয়।

ডিজিটাল ডিভাইসে কোনো সার্কিটে বিদ্যুতের উপস্থিতিকে ১ ধরা হয় এবং বিদ্যুতের অনুপস্থিতিকে ০ ধরা হয়। ডিজিটাল সিস্টেমে ভোল্টেজ লেভেল ০ থেকে .৮ ভোল্টকে লজিক ০ ধরা হয় এবং ভোল্টেজ লেভেল  ২ থেকে  ৫  ভোল্টকে লজিক  ১  ধরা হয়। ডিজিটাল সিস্টেমে +০.৮  ভোল্ট থেকে  +২  ভোল্ট লেভেল সংজ্ঞায়িত নয় বিধায় ব্যবহার করা হয় না।

বুলিয়ান অ্যালজেবরার বৈশিষ্ট্যঃ 

• বুলিয়ান অ্যালজেবরায় মাত্র দুটি অঙ্ক ‘০’ এবং ‘১’ ব্যবহৃত হয়।
• বুলিয়ান চলকের দুটি মান থাকায় বুলিয়ান অ্যালজেবরা দশমিক অ্যালজেবরার তুলনায় অনেক সহজ পদ্ধতি।
• বুলিয়ান অ্যালজেবরায় কোনো  ধরনের ভগ্নাংশ, লগারিদম, বর্গ, ঋণাত্মক সংখ্যা, কাল্পনিক সংখ্যা ইত্যাদি ব্যবহার করা যায় না।
• বুলিয়ান অ্যালজেবরায় শুধু মাত্র যৌক্তিক যোগ, গুণ ও পূরকের মাধ্যমে সমস্ত গাণিতিক কাজ করা হয়।
• বুলিয়ান অ্যালজেবরায় কোনো ধরনের জ্যামিতিক বা ত্রিকোণমিতিক সূত্র ব্যবহার করা যায় না।

বুলিয়ান অ্যালজেবরায় নিমোক্ত উপাদানগুলো রয়েছে-

প্রতীক বা মৌলিক চিহ্নঃ দুটি –  TRUE/ON/1 এবং FALSE/OFF/0

অপারেটরঃ তিনটি-  AND ( . ), OR ( + ), NOT( ¯ )

মৌলিক অপারেশনঃ 

অ্যান্ড অপারেশন (AND Operation) বা যৌক্তিক গুণ (Logical Multiplication)

অর অপারেশন (OR Operation) বা যৌক্তিক যোগ (Logical Addition)

নট অপারেশন (NOT Operation) বা যৌক্তিক পূরক (Logical Inversion)

উপপাদ্য/ সূত্র/নিয়মাবলীঃ বুলিয়ান উপাপাদ্য, ডি-মরগ্যান উপাপাদ্য, দ্বৈতনীতি ইত্যাদি

 

বুলিয়ান চলকঃ বুলিয়ান অ্যালজেবরায় যে রাশির মান পরিবর্তনশীল তাকে বুলিয়ান চলক বলে। যেমন- C = A + B, এখানে A ও B হচ্ছে বুলিয়ান চলক।

বুলিয়ান ধ্রুবকঃ বুলিয়ান অ্যালজেবরায় যে রাশির মান অপরিবর্তনশীল থাকে তাকে বুলিয়ান  ধ্রুবক বলে।

যেমন- Y = A+ 0 + 1,  এখানে 0 এবং 1 হচ্ছে বুলিয়ান  ধ্রুবক।

ধ্রুবকের মান সব সময় অপরিবর্তিত থাকে কিন্তু চলকের মান পরিবর্তিত হয়। বিভিন্ন ইলেকট্রনিক বর্তনীর ইনপুট ও আউটপুটের লজিক অবস্থা নির্দিষ্ট করার জন্য বুলিয়ান চলক ও ধ্রুবক ব্যবহার করা হয়।

বুলিয়ান পূরক: বুলিয়ান অ্যালজেবরায় যেকোনো  চলকের মান  ০ অথবা  ১ হয়। এই  ০ এবং  ১  কে একটি অপরটির বুলিয়ান পূরক বলা হয়। বুলিয়ান পূরকে ‘–’  চিহ্নের মাধ্যমে প্রকাশ করা হয়। গণিতের ভাষায় লেখা হয় A এর পূরক A′।

 

বুলিয়ান স্বতঃসিদ্ধঃ

বুলিয়ান অ্যালজেবরায় সমস্ত গাণিতিক কাজ শুধুমাত্র যৌক্তিক যোগ, গুণ ও পূরকের সাহায্যে করা হয়। বুলিয়ান অ্যালজেবরায় যৌক্তিক যোগ, গুণ ও পূরকের নিয়মগুলোকে বুলিয়ান স্বতঃসিদ্ধ বলে। বুলিয়ান স্বতঃসিদ্ধ গুলো-

• যোগের বুলিয়ান স্বতঃসিদ্ধ (Boolean Postulates of OR)
• গুণের বুলিয়ান স্বতঃসিদ্ধ (Boolean Postulates of AND)
• পূরকের বুলিয়ান স্বতঃসিদ্ধ (Boolean Postulates of NOT)

যোগের বুলিয়ান স্বতঃসিদ্ধঃ যৌক্তিক যোগের সময় বুলিয়ান অ্যালজেবরা যেসব নিয়ম মেনে চলে তাকে যোগের বুলিয়ান স্বতঃসিদ্ধ বলে। যৌক্তিক যোগের সময় বুলিয়ান চলকগুলোর মানের মধ্যে OR(+) অপারেটর ব্যবহার করা হয় তা প্রচলিত যোগের চিহ্ন নয়। বুলিয়ান অ্যালজেবরায় এ যোগ চিহ্নকে যৌক্তিক যোগ হিসেবে ব্যবহার করা হয়। যৌক্তিক যোগের চারটি নিয়ম প্রচলিত। যথা−

0 + 0 = 0

0 + 1 = 1

1 + 0 = 1

1 + 1 = 1

উপরের বুলিয়ান স্বতঃসিদ্ধ থেকে বলা যায় যে, বুলিয়ান অ্যালজেবরায় যৌক্তিক যোগের ক্ষেত্রে যেকোনো একটির মান ১ হলে যৌক্তিক যোগফল ১ হবে, অন্যথায় ০ হবে।

গুণের বুলিয়ান স্বতঃসিদ্ধ: যৌক্তিক গুণের সময় বুলিয়ান অ্যালজেবরা যেসব নিয়ম মেনে চলে তাকে গুণের বুলিয়ান স্বতঃসিদ্ধ বলে। যৌক্তিক গুণের সময় বুলিয়ান চলকগুলোর মানের মধ্যে AND(.) অপারেট ব্যবহার করা হয়। যৌক্তিক গুণের চারটি নিয়ম প্রচলিত। যথা:

0 . 0   = 0

0 . 1   = 0

1 . 0   = 0

1 . 1   = 1

উপরের বুলিয়ান স্বতঃসিদ্ধ থেকে বলা যায় যে, বুলিয়ান অ্যালজেবরায় যৌক্তিক গুণের ক্ষেত্রে যেকোনো একটির মান  ০  হলে যৌক্তিক গুণফল  ০  হবে, অন্যথায়  ১  হবে।

পূরকের বুলিয়ান স্বতঃসিদ্ধ: যৌক্তিক পূরকের সময় বুলিয়ান অ্যালজেবরা যেসব নিয়ম মেনে চলে তাকে পূরকের বুলিয়ান স্বতঃসিদ্ধ বলে। যৌক্তিক পূরকের সময় বুলিয়ান চলকগুলোর উপর পূরক চিহ্ন ( ¯ ) ব্যবহার করা হয়। বুলিয়ান অ্যালজেবরায় যৌক্তিক পূরকের ক্ষেত্রে ০ থাকলে ১ হয়, এবং ১ থাকলে ০ হয়।

1´ = 0

0´ = 1

 

বুলিয়ান দ্বৈতনীতি: বুলিয়ান অ্যালজেবরায় ব্যবহৃত সকল উপপাদ্য বা সমীকরণ যে দুটি নিয়ম মেনে একটি বৈধ্য সমীকরণ থেকে অপর একটি বৈধ্য সমীকরণ নির্ণয় করা যায় তাকে বুলিয়ান দ্বৈতনীতি বলে। অর্থাৎ বুলিয়ান অ্যালজেবরায় অর  (OR)  এবং অ্যান্ড  (AND) এর সাথে সম্পর্কযুক্ত সকল উপপাদ্য বা সমীকরণ দ্বৈতনীতি মেনে চলে। এ নিয়ম দু টি হলো −

১।  ০ এবং ১ পরস্পর বিনিময় করে অর্থাৎ ০ এর পরিবর্তে ১ এবং ১ এর পরিবর্তে ০ ব্যবহার করে।

২। অর (+) এবং অ্যান্ড (.) পরস্পর বিনিময় করে অর্থাৎ অর (+) এর পরিবর্তে অ্যান্ড (.) এবং অ্যান্ড (.) এর পরিবর্তে অর (+) ব্যবহার করে।

উদাহরণ: ১ + ১ = ১ সমীকরণে ১ এর পরিবর্তে ০ এবং (+) এর পরিবর্তে (.) বসিয়ে পাই ০.০ = ০ এটাও একটি বৈধ্য সমীকরণ। আবার ০.১ = ০  সমীকরণে  ০  এর পরিবর্তে  ১  ও  ১ এর পরিবর্তে  ০ এবং (.) এর পরিবর্তে (+) বসিয়ে পাই ১ + ০ =১ এটাও একটি বৈধ্য সমীকরণ।

 

বুলিয়ান উপপাদ্যঃ

১৯৪০ সালে E.V Huntington বুলিয়ান অ্যালজেবরার জন্য কিছু উপপাদ্য তৈরি করেন, যার সাহায্যে বুলিয়ান অ্যালজেবরার জটিল সমীকরণকে সরলীকরণ করা যায়। এই উপপাদ্যগুলোকে হানটিংটন উপপাদ্য বলা হয়।

মৌলিক উপপাদ্য(Basic Theorem): 

বুলিয়ান উপপাদ্যসমূহের সুইচিং সার্কিটঃ 

Boolean Theorem	Equivalent Switching Circuit
A + 1 = 1
A . 0 = 0
A + 0 = A
A . 1 = A
A + A = A
A . A = A
A + A = 1
A . A = 0
A+B = B+A
A.B = B.A

বুলিয়ান যোগের ক্ষেত্রে মৌলিক উপপাদ্যসমূহের প্রমানঃ

বুলিয়ান গুণের ক্ষেত্রে মৌলিক উপপাদ্যসমূহের প্রমানঃ

 

ডি-মরগ্যানের উপপাদ্যঃ

ফরাসি গণিতবিদ ডি-মরগ্যান, বুলিয়ান ফাংশন সরলীকরণ করার জন্য দুটি সূত্র আবিষ্কার করেন।

প্রথম উপপাদ্যঃ যেকোন সংখ্যক চলকের যৌক্তিক যোগের পূরক বা কমপ্লিমেন্ট , প্রত্যেক চলকের পূরক বা কমপ্লিমেন্টের যৌক্তিক গুণের সমান। n সংখ্যক চলকের জন্য প্রথম উপপাদ্য-

দ্বিতীয় উপপাদ্যঃ যেকোন সংখ্যক চলকের যৌক্তিক গুণের পূরক বা কমপ্লিমেন্ট, প্রত্যেক চলকের পূরক বা কমপ্লিমেন্টের যৌক্তিক যোগের সমান। n সংখ্যক চলকের জন্য দ্বিতীয় উপপাদ্য –

A ও B দুটি চলকের জন্য ডি-মরগ্যানের উপপাদ্য দুটি নিম্নরূপ−

A ,B ও C তিনটি চলকের জন্য ডি-মরগ্যানের উপপাদ্য দুটি নিম্নরূপ−

 

সত্যক সারণি: 

যে সারণির মাধ্যমে বুলিয়ান সমীকরণে চলকসমূহের বিভিন্ন মানবিন্যাসের জন্য বিভিন্ন আউটপুট প্রদর্শন করা হয়, তাকে সত্যক সারণি বলে। সত্যক সারণির সাহায্যে বুলিয়ান সমীকরণের সত্যতা যাচাই করা হয়।

যদি বুলিয়ান সমীকরণে n সংখ্যক চলক থাকে, তবে সত্যক সারণিতে ইনপুট কম্বিনেশন হবে 2n সংখ্যক এবং আউটপুটও হবে 2n সংখ্যক।

উদাহরনঃ একটি অর(OR) লজিক গেইটের ইনপুট চলক A ও B এর সাপেক্ষে আউটপুট ফাংশন F= A+B এর সত্যক সারণি দেখানো হল। যেহেতু চলক দুইটি (A ও B) তাই ইনপুট সেট ২২=৪ টি হবে।

চিত্রঃ F= A+B এর সত্যক সারণি

 

সত্যক সারণি থেকে আউটপুটের বুলিয়ান এক্সপ্রেশন বা সমীকরণ লেখার উপায়ঃ 

সত্যক সারণির বুলিয়ান ফাংশন দুই ভাবে নির্ণয় করা যায়। যথা-

• মিনটার্মের সাহায্যে
• ম্যাক্সটার্মের সাহায্যে

মিনটার্মের সাহায্যে সারণির বুলিয়ান ফাংশন নির্ণয়ঃ 

সত্যক সারণিতে ব্যবহৃত ইনপুট বিন্যাসসমূহের গুণফলকে বলা হয় মিনটার্ম। প্রতিটি মিনটার্মের মান ১ হয়। সত্যক সারণির যেসব মিনটার্মের আউটপুট মান ১, সেই মিনটার্মসমূহ যোগ করে বুলিয়ান ফাংশন নির্ণয় করা হয়। এ পদ্ধতিকে SOP(Sum of Products) বলা হয়।

ম্যাক্সটার্মের সাহায্যে সারণির আউটপুট ফাংশন নির্ণয়ঃ  

সত্যক সারণিতে ব্যবহৃত ইনপুট বিন্যাসসমূহের যোগফলকে বলা হয় ম্যাক্সটার্ম। প্রতিটি ম্যাক্সটার্মের মান ০ হয়। সত্যক সারণির যেসব ম্যাক্সটার্মের আউটপুট মান ০, সেই ম্যাক্সটার্মসমূহ গুণ করে আউটপুট ফাংশন বা সমীকরণ নির্ণয় করা হয়। এ পদ্ধতিকে POS (Product of Sums) বলা হয়।

অর্থাৎ উভয় প্রক্রিয়ায় একই বুলিয়ান ফাংশন পাওয়ার যায়।

 

সত্যক সারণির সাহায্যে বুলিয়ান সমীকরন বা উপপাদ্যের প্রমানঃ

সত্যক সারণির সাহায্যে বুলিয়ান সমীকরণ প্রমাণের জন্য নিমোক্ত ধাপসমূহ অনুসরণ করা হয়-

১। বুলিয়ান সমীকরণটিতে ব্যবহৃত মোট চলক সংখ্যা নির্ণয় করতে হয়। n সংখ্যক চলকের জন্য সত্যক সারণিতে ২n সংখ্যক ভিন্ন ভিন্ন ইনপুট সেট হয়।

২। সত্যক সারণির মূল কাঠামো তৈরির জন্য সমীকরণে যতোগুলো চলক আছে ততোগুলো কলাম এবং ২n সংখ্যক ভিন্ন ভিন্ন ইনপুট সেট দেওয়ার জন্য ২n সংখ্যক সারি বা রো তৈরি করতে হয়।

৩। সমীকরণের বামপক্ষ ও ডানপক্ষ সমান প্রমাণের জন্য বামপক্ষ ও ডানপক্ষের সকল প্রোডাক্ট টার্ম নির্নয় করতে হয়।প্রোডাক্ট টার্ম নির্নয় করার জন্য প্রয়োজনীয় সাব-প্রোডাক্ট টার্ম নির্নয় করতে হয়। এক্ষেত্রে বিভিন্ন সাব-প্রোডাক্ট টার্ম বা প্রোডাক্ট টার্ম নির্নয়ের জন্য অতিরিক্ত কলাম তৈরি করতে হয়।

 

A ও B  দুইটি চলকের জন্য ডি-মরগ্যানের উপপাদ্যদুটি সত্যক সারণির সাহায্যে প্রমাণঃ 

A , B ও C  তিনটি চলকের জন্য ডি-মরগ্যানের উপপাদ্যের প্রমাণ

বুলিয়ান ফাংশন লজিক গেইটের মাধ্যমে বাস্তবায়ন করা হয়। এক্ষেত্রে ফাংশনে লজিক অপারেটরের সংখ্যা কম থাকলে বাস্তবায়নের ক্ষেত্রে লজিক গেইটের সংখ্যা কম লাগে। ফলে বাস্তবায়ন সহজ হয় এবং অর্থ সাশ্রয় হয়। তাই বিভিন্ন বুলিয়ান উপপাদ্যের সাহায্যে বুলিয়ান ফাংশন সরলীকরণ করা হয়।

বুলিয়ান উপপাদ্যের সাহায্যে বুলিয়ান রাশিমালা সরলীকরণের ক্ষেত্রে নিমোক্ত নিয়ম বা ক্রম মানা হয়ঃ

• প্রথমত, সমীকরণের বামদিক থেকে ডানদিকে সরলীকরণ শুরু করতে হবে।
• দ্বিতীয়ত, বন্ধনীর “()” ভিতরের কাজগুলো করতে হবে।
• তৃতীয়ত, বুলিয়ান অ্যালজেবরার মৌলিক অপারেশনগুলো NOT, AND, OR এর কাজ পর্যায়ক্রমে সম্পন্ন করতে হবে।
• সরলীকরণের একটি নির্দিস্ট ধাপে যদি কোন উপপাদ্য প্রয়োগ না করা যায় তবে বুঝতে হবে সমীকরণটি আর সরল করা যাবে না।

 

 

লজিক গেইট: লজিক গেইট হলো এক ধরনের ইলেকট্রনিক সার্কিট যা এক বা একাধিক ইনপুট গ্রহণ করে এবং একটি মাত্র  আউটপুট প্রদান করে। লজিক গেইট বুলিয়ান অ্যালজেবরায় মৌলিক কাজগুলো বাস্তবায়নের জন্য ব্যবহার করা হয় । IC এর মুলে রয়েছে লজিক গেইট এবং লজিক গেইট হচ্ছে বুলিয়ান অ্যালজেবরার ব্যবহারিক প্রয়োগ।

লজিক গেইটের প্রকারভেদঃ 

মৌলিক লজিক গেইটঃ যেসকল গেইট দ্বারা বুলিয়ান অ্যালজেবরার মৌলিক অপারেশনগুলো বাস্তবায়ন করা যায় তাদেরকে মৌলিক লজিক গেইট বলা হয়। মৌলিক লজিক গেইটের সাহায্যে সকল যৌগিক গেইট ও যেকোন সার্কিট তৈরি করা যায়। ডিজিটাল ইলেক্ট্রনিক্সে মৌলিক লজিক গেইট তিনটি। যথা-

• অর গেইট (OR Gate)
• অ্যান্ড গেইট (AND Gate)
• নট গেইট (NOT Gate)

অর গেইট (OR Gate):

OR গেইট হচ্ছে যৌক্তিক যোগের গেইট। অর্থাৎ বুলিয়ান অ্যালজেবরায় যৌক্তিক যোগের কাজ সম্পাদনের জন্য যে গেইট ব্যবহার করা হয়, তাকে OR গেইট বলা হয়। OR গেইটে দুই বা ততোধিক ইনপুট লাইন থাকে এবং একটিমাত্র আউটপুট লাইন থাকে। যেহেতু OR গেইট যৌক্তিক যোগের গেইট তাই এটি যৌক্তিক যোগের নিয়ম মেনে চলে। অর্থাৎ এই গেইটের ক্ষেত্রে যেকোনো একটি ইনপুটের মান ১ হলে আউটপুট ১ হয়, অন্যথায় ০ হয়।

OR গেইটের সুইচিং সার্কিটের সুইচগুলো সমান্তরালে সমবায়ে যুক্ত থাকে। ফলে যেকোন একটি সুইচ অন(1) থাকলে বাল্বটি জ্বলে।

 

দুই ইনপুট(A & B) বিশিষ্ট OR গেইটঃ

তিন ইনপুট(A, B & C) বিশিষ্ট OR গেইটঃ

 

অ্যান্ড গেইট (AND Gate):

AND গেইট হচ্ছে যৌক্তিক গুণের গেইট। অর্থাৎ বুলিয়ান অ্যালজেবরায় যৌক্তিক গুণের কাজ সম্পাদনের জন্য যে গেইট ব্যবহার করা হয়, তাকে AND গেইট বলা হয়। AND গেইটের ক্ষেত্রে দুই বা ততোধিক ইনপুট লাইন থাকে এবং একটি মাত্র আউটপুট লাইন থাকে।  যেহেতু AND গেইট যৌক্তিক গুণের গেইট তাই এটি যৌক্তিক গুণের নিয়ম মেনে চলে। অর্থাৎ এই গেইটের ক্ষেত্রে যেকোনো একটি ইনপুটের মান ০ হলে আউটপুট ০ হয়, অন্যথায় ১ হয়।

AND গেইটের সুইচিং সার্কিটের সুইচগুলো শ্রেণি সমবায়ে যুক্ত থাকে। ফলে যেকোন একটি অফ(0) থাকলে বাল্বটি জ্বলে না।

দুই ইনপুট(A & B) বিশিষ্ট AND গেইটঃ

তিন ইনপুট(A, B & C) বিশিষ্ট AND গেইটঃ

নট গেইট (NOT Gate):

NOT গেইট হচ্ছে যৌক্তিক পূরকের গেইট। একে ইনভার্টার ও বলা হয়। অর্থাৎ বুলিয়ান অ্যালজেবরায় যৌক্তিক পূরকের কাজ সম্পাদনের জন্য যে গেইট ব্যবহার করা হয়, তাকে NOT গেইট বলা হয়। এই গেইটে একটি মাত্র ইনপুট লাইন এবং একটি মাত্র আউটপুট লাইন থাকে। যেহেতু NOT গেইট যৌক্তিক পূরকের গেইট তাই এটি যৌক্তিক পূরকের নিয়ম মেনে চলে। এই গেইটের ক্ষেত্রে আউটপুট হয় ইনপুটের বিপরীত। অর্থাৎ ইনপুট সংকেত ১ হলে আউটপুট সংকেত ০ হয় অথবা ইনপুট সংকেত ০ হলে আউটপুট সংকেত ১ হয়।

NOT গেইটের সুইচিং সার্কিটে একটিমাত্র  সুইচ থাকে যা বাল্ব এর সাথে সমান্তরাল সমবায়ে যুক্ত থাকে। ফলে সুইচটি অফ(0) থাকলে বাল্বটি জ্বলে কিন্তু সুইচটি অন(1) থাকলে বাল্বটি জ্বলে না।

যৌগিক গেইট:

দুই বা ততোধিক মৌলিক গেইটের সাহায্যে যে গেইট তৈরি করা হয় তাকে যৌগিক গেইট বলে। যেমন- AND Gate +NOT Gate = NAND Gate,  OR Gate + NOT Gate = NOR Gate। যৌগিক গেইটকে দুই ভাগে ভাগ করা যায়। যেমন-

• সার্বজনীন গেইট (NOR ও NAND)
• বিশেষ গেইট (X-OR ও X-NOR)

সার্বজনীন গেইট:  

যে গেইট এর সাহায্যে মৌলিক গেইটসহ (AND,OR,NOT) যেকোন গেইট এবং যেকোন সার্কিট বাস্তবায়ন করা যায় তাকে সার্বজনীন গেইট বলে। NAND ও NOR গেইটকে কে সার্বজনীন গেইট বলা হয়। কারণ শুধুমাত্র NAND গেইট বা শুধুমাত্র NOR গেইট দিয়ে মৌলিক গেইটসহ যেকোনো লজিক গেইট বা সার্কিট বাস্তবায়ন করা যায়। সার্বজনীন গেইট তৈরিতে খরচ কম বিধায় ডিজিটাল সার্কিটে এই গেইট বেশি ব্যবহৃত হয়।

চিত্রঃ সার্বজনীন গেইট

নর গেইট (NOR Gate):

NOR গেইট একটি যৌগিক গেইট যা OR গেইট ও NOT গেইটের সমন্বয়ে তৈরি। OR গেইটের আউটপুটকে NOT গেইটের মধ্য দিয়ে প্রবাহিত করলে NOR গেইট পাওয়া যায়। OR গেইটের আউটপুটকে উল্টিয়ে দিলে NOR গেইটের আউটপুট পাওয়া যায়।

চিত্রঃ OR Gate + NOT Gate = NOR Gate

NOR গেইটে দুই বা ততোদিক ইনপুট লাইন থাকে এবং একটি মাত্র আউটপুট লাইন থাকে। NOR গেইট কে যৌগিক গেইট  এবং সার্বজনীন গেইটও বলা হয়।

 

দুই ইনপুট(A & B) বিশিষ্ট NOR গেইটঃ

তিন ইনপুট(A, B & C) বিশিষ্ট NOR গেইটঃ

 

ন্যান্ড গেইট (NAND Gate):

NAND গেইট একটি যৌগিক গেইট যা AND গেইট ও NOT গেইটের সমন্বয়ে তৈরি। AND গেইটের আউটপুটকে NOT গেইটের মধ্য দিয়ে প্রবাহিত করলে NAND গেইট পাওয়া যায়। অর্থাৎ AND গেইটের আউটপুটকে উল্টিয়ে দিলে NAND গেইটের আউটপুট পাওয়া যায়।

চিত্রঃ AND Gate + NOT Gate = NAND Gate

NAND গেইটে দুই বা ততোদিক ইনপুট লাইন থাকে এবং একটি মাত্র আউটপুট লাইন থাকে। NAND গেইট কে যৌগিক গেইট  এবং সার্বজনীন গেইটও বলা হয়।

 

দুই ইনপুট(A & B) বিশিষ্ট NAND গেইটঃ

 

তিন ইনপুট(A, B & C) বিশিষ্ট NAND গেইটঃ

বিশেষ গেইটঃ

X-OR ও X-NOR গেইট দুটিকে বলা হয় বিশেষ গেইট।

চিত্রঃ বিশেষ গেইট

X-OR গেইটঃ

Exclusive OR গেইটকে সংক্ষেপে X-OR গেইট বলা হয়। এটি একটি যৌগিক গেইট যা AND, OR ও NOT গেইটের সমন্বয়ে তৈরি। এই গেইটের মাধ্যমে বিভিন্ন ইনপুট বিট তুলনা করে আউটপুট সংকেত পাওয়া যায়। ইনপুটে বিজোড় সংখ্যক ১ থাকলে আউটপুট ১ হয়, অন্যথায় ০ হয়। X-OR অপারেশনকে ⊕ চিহ্ন দ্বারা প্রকাশ করা হয়।

X-OR গেইটে দুই বা ততোদিক ইনপুট লাইন থাকে এবং একটি মাত্র আউটপুট লাইন থাকে। X-OR গেইট কে যৌগিক গেইট  এবং বিশেষ গেইটও বলা হয়।

 

দুই ইনপুট(A & B) বিশিষ্ট XOR গেইটঃ

XOR গেইটের সত্যক সারণি থেকে SOP মেথডের সাহায্যে নিম্নরূপ বুলিয়ান ফাংশন লিখতে পারি-

 F = A´ B + A B´

বুলিয়ান ফাংশনটিকে বাস্তবায়ন করে পাই-

চিত্রঃ মৌলিক গেইট দিয়ে X-OR গেইট বাস্তবায়ন 

তিন ইনপুট(A, B & C) বিশিষ্ট XOR গেইটঃ

XOR গেইটের সত্যক সারণি থেকে SOP মেথডের সাহায্যে নিম্নরূপ বুলিয়ান ফাংশন লিখতে পারি-

F = A´B´C + A´BC´ + AB´C´ + ABC

উপরের বুলিয়ান ফাংশনটি বাস্তবায়ন কর।

X-NOR গেইটঃ 

Exclusive NOR গেইটকে সংক্ষেপে X-NOR গেইট বলা হয়। এটি একটি যৌগিক গেইট যা AND, OR ও NOT গেইটের সমন্বয়ে তৈরি। X-OR গেইটের আউটপুট NOT গেইটের মধ্যে প্রবাহিত করলে X-NOR গেইট পাওয়া যায়। অর্থাৎ X-OR গেইটের আউটপুটকে উল্টিয়ে দিলে X-NOR গেইটের আউটপুট পাওয়া যায়। অর্থাৎ ইনপুটে বিজোড় সংখ্যক ১ থাকলে আউটপুট ০ হয়, অন্যথায় ১ হয়।

চিত্রঃ XOR Gate + NOT Gate = XNOR Gate

X-NOR গেইটে দুই বা ততোদিক ইনপুট লাইন থাকে এবং একটি মাত্র আউটপুট লাইন থাকে। X-NOR গেইট কে যৌগিক গেইট  এবং বিশেষ গেইটও বলা হয়।

দুই ইনপুট(A & B) বিশিষ্ট XNOR গেইটঃ

XNOR গেইটের সত্যক সারণি থেকে SOP মেথডের সাহায্যে নিম্নরূপ বুলিয়ান ফাংশন লিখতে পারি-

 F = A´B´ + AB

বুলিয়ান ফাংশনটিকে বাস্তবায়ন করে পাই –

চিত্রঃ মৌলিক গেইট দিয়ে X-NOR গেইট বাস্তবায়ন 

 

তিন ইনপুট(A, B & C) বিশিষ্ট XNOR গেইটঃ

XNOR গেইটের সত্যক সারণি থেকে SOP মেথডের সাহায্যে নিম্নরূপ বুলিয়ান ফাংশন লিখতে পারি-

 F = A´B´C´ + A´BC + AB´C + ABC´

বুলিয়ান ফাংশনটি বাস্তবায়ন কর।

NAND গেইটের সার্বজনীনতা এর প্রমানঃ  

শুধুমাত্র NAND গেইট দিয়ে NOT গেইট বাস্তবায়ন:

শুধুমাত্র NAND গেইট দিয়ে AND গেইট বাস্তবায়ন:

শুধুমাত্র NAND গেইট দিয়ে OR গেইট বাস্তবায়ন:

উপরের আলোচনা থেকে দেখতে পাই শুধুমাত্র NAND গেইট দ্বারা তিনটি মৌলিক গেইট বাস্তবায়ন করা যায়। আবার আমরা জানি তিনটি মৌলিক গেইট দ্বারা যেকোনো গেইট অথবা যেকোনো সার্কিট বাস্তবায়ন করা যায়। যেহেতু NAND গেইট দ্বারা তিনটি মৌলিক গেইটসহ (AND, OR, NOT ) যেকোনো গেইট অথবা যেকোনো সার্কিট বাস্তবায়ন করা যায়, তাই NAND গেইটকে সার্বজনীন গেইট বলে।

 

NOR গেইটের সার্বজনীনতা এর প্রমানঃ 

শুধুমাত্র NOR গেইট দিয়ে NOT গেইট বাস্তবায়ন:

শুধুমাত্র NOR গেইট দিয়ে OR গেইট বাস্তবায়ন:

শুধুমাত্র NOR গেইট দিয়ে AND গেইট বাস্তবায়ন:

উপরের আলোচনা থেকে দেখতে পাই শুধুমাত্র NOR গেইট দ্বারা তিনটি মৌলিক গেইট বাস্তবায়ন করা যায়। আবার আমরা জানি তিনটি মৌলিক গেইট দ্বারা যেকোনো গেইট অথবা যেকোনো সার্কিট বাস্তবায়ন করা যায়। যেহেতু NOR গেইট দ্বারা তিনটি মৌলিক গেইটসহ (AND,OR,NOT) যেকোনো গেইট অথবা যেকোনো সার্কিট বাস্তবায়ন করা যায়, তাই NOR গেইটকে সার্বজনীন গেইট বলে।

 

[যেকোন ফাংশন NAND এর সাহায্যে বাস্তবায়ন করার সময় দেখতে হবে ফাংশনে কোন OR অপারেটর আছে কিনা? যদি থাকে তাহলে ডি-মরগ্যান সূত্রের মাধ্যমে OR কে AND রূপান্তর করে তারপর বাস্তবায়ন করতে হবে।]

শুধুমাত্র NAND গেইট দ্বারা দুই চলক বিশিষ্ট X-OR গেইট বাস্তবায়নঃ

A ও B চলকের ক্ষেত্রে XOR গেইটের বুলিয়ান ফাংশন,  

শুধুমাত্র NAND গেইট দ্বারা দুই চলক বিশিষ্ট X-NOR গেইট বাস্তবায়নঃ 

A ও B চলকের ক্ষেত্রে XNOR গেইটের বুলিয়ান ফাংশন,  

 

[যেকোন ফাংশন NOR এর সাহায্যে বাস্তবায়ন করার সময় দেখতে হবে ফাংশনে কোন AND অপারেটর আছে কিনা? যদি থাকে তাহলে ডি-মরগ্যান সূত্রের মাধ্যমে  AND কে OR রূপান্তর করে তারপর বাস্তবায়ন করতে হবে।]

শুধুমাত্র NOR গেইট দ্বারা দুই চলক বিশিষ্ট X-OR গেইট বাস্তবায়নঃ 

A ও B চলকের ক্ষেত্রে XOR গেইটের বুলিয়ান ফাংশন,  

শুধুমাত্র NOR গেইট দ্বারা দুই চলক বিশিষ্ট X-NOR গেইট বাস্তবায়নঃ

A ও B চলকের ক্ষেত্রে XNOR গেইটের বুলিয়ান ফাংশন, 

 

নিচের ফাংশনগুলো শুধুমাত্র NAND অথবা শুধুমাত্র NOR গেইট এর সাহায্যে বাস্তবায়ন করঃ 

লজিক ফাংশন থেকে লজিক সার্কিট তৈরি বা বাস্তবায়ন: 

• লজিক ফাংশনটি শুধুমাত্র মৌলিক গেইটের সাহায্যে বাস্তবায়ন করতে হতে পারে।
• লজিক ফাংশনটি শুধুমাত্র সার্বজনীন গেইটের সাহায্যে বাস্তবায়ন করতে হতে পারে।
• লজিক ফাংশনটি যেকোন প্রকার গেইট ব্যবহার করে বাস্তবায়ন করতে হতে পারে।
• লজিক ফাংশনটি সরলীকরণ করে তারপর মৌলিক বা সার্বজনীন গেইট দ্বারা বাস্তবায়ন করতে হতে পারে।

 

লজিক ফাংশনটি মৌলিক গেইটের সাহায্যে বাস্তবায়ন করতে নিমোক্ত নিয়ম বা ক্রম মানা হয়ঃ

• যদি ফাংশনটি সরল করতে হয়, তাহলে প্রথমেই সরল করতে হবে।
• ফাংশনে যতগুলো চলক থাকবে তাদের প্রত্যেকটির জন্য কমন লাইন আঁকতে হবে।
• বামদিক থেকে ফাংশনের মৌলিক অপারেশনগুলো NOT, AND, OR এর কাজ পর্যায়ক্রমে সম্পন্ন করতে হবে। এক্ষেত্রে বন্ধনীর “()” ভিতরের কাজগুলো প্রায়োরিটি দিতে হবে।

 

উদাহরণ-১ঃ নিচের ফাংশনটি শুধুমাত্র মৌলিক গেইটের সাহায্যে বাস্তবায়ন কর।

সমাধানঃ 

 

 

 

 

 

 

 

 

 

উদাহরণ-২ঃ নিচের ফাংশনটি বাস্তবায়ন কর।

সমাধানঃ 

 

লজিক সার্কিট থেকে লজিক ফাংশন তৈরি/বাস্তবায়নঃ

• লজিক সার্কিট থেকে লজিক ফাংশন নির্নয় করে তা সরল করতে হতে পারে।
• লজিক সার্কিট থেকে সরলীকৃত ফাংশন নির্নয় এবং তা মৌলিক বা সার্বজনীন গেইট দ্বারা বাস্তবায়ন করতে হতে পারে।

 

উদাহরণ-১ঃ নিমোক্ত সার্কিটির সরলীকৃত ফাংশন নির্নয় কর।

সমাধানঃ 

 

উদাহরণ-২ঃ নিমোক্ত সার্কিটির সরলীকৃত ফাংশন বাস্তবায়ন কর।

সমাধানঃ 

সরলীকৃত ফাংশন বাস্তবায়ন করে পাই-

 

FIG: Radio metrix 4 Bit Encoder/Decoder IC for Remote.

এনকোডার: এনকোডার এক ধরনের সমবায় সার্কিট বা ডিজিটাল বর্তনী যা মানুষের ব্যবহৃত বিভিন্ন আলফানিউমেরিক বর্ণ, বিশেষ চিহ্ন, টেক্সট, অডিও ও ভিডিও ইত্যাদিকে কম্পিউটার বা ডিজিটাল সিস্টেমের বোধগম্য কোডে রূপান্তর করে।

অন্যভাবে বলা যায় এটি একটি ডিজিটাল বর্তনী যা এনকোডিং এর জন্য ব্যবহৃত হয়। অর্থাৎ এনকোডার অ্যানালগ সিগন্যালকে ডিজিটাল সিগন্যালে রূপান্তরিত করে।

এনকোডারের বৈশিষ্ট্যসমূহঃ

• এ বর্তনীর 2n  সংখ্যক ইনপুট লাইন থেকে সর্বাধিক n সংখ্যক আউটপুট লাইন পাওয়া যায়।
• যেকোনো মুহূর্তে একটি মাত্র ইনপুট ১ এবং বাকি সকল ইনপুট ০ থাকে।
• এনকোডার ডিকোডারের বিপরীত কাজ সম্পাদন করে।
• এনকোডার সাধারণত ইনপুট ডিভাইস অর্থাৎ কী-বোর্ডের সাথে যুক্ত থাকে।

চিত্রঃ এনকোডারের ব্লক চিত্র

4 to 2 লাইন এনকোডার:

ধরি 4 to 2 এনকোডারের চারটি ইনপুট D0, D1, D2 ও D3 এবং দুটি আউটপুট X ও Y। নিচে 4 to 2 লাইন এনকোডারের ব্লক চিত্র দেখানো হলো-

চিত্রঃ 4 to 2 লাইন এনকোডারের ব্লক চিত্র  

যেকোনো মুহূর্তে চারটি ইনপুটের মধ্যে একটি মাত্র ইনপুট ১ এবং বাকি সকল ইনপুট ০ থাকে। নিচে 4 to 2 লাইন এনকোডারের সত্যক সারণি দেখানো হলো-

চিত্রঃ 4 to 2 লাইন এনকোডারের সত্যক সারণি

সত্যক সারণি থেকে প্রত্যেকটি আউটপুটের জন্য নিমোক্ত বুলিয়ান ফাংশন লিখা যায়-

X=D2+D3

Y=D1+D3

দুই ইনপুট বিশিষ্ট OR গেইট ব্যবহার করে উপরের ফাংশন দুটি বাস্তবায়ন করা যায়। নিচে 4 to 2 লাইন এনকোডারের সার্কিট দেখানো হলো-

চিত্রঃ 4 to 2 লাইন এনকোডারের সার্কিট

উপরের সার্কিটটি দুটি OR গেইটের সমন্বয়ে তৈরি, যা চারটি ইনপুটকে দুই বিটে এনকোড করতে পারে।

অক্টাল টু বাইনারি এনকোডার অথবা 8 to 3 লাইন এনকোডারঃ

8 to 3 এনকোডারের আঁটটি ইনপুট D0 to D7 এবং তিনটি আউটপুট X , Y ও Z। নিচে 8 to 3 এনকোডারের ব্লক চিত্র দেখানো হলো-

চিত্রঃ 8 to 3 লাইন এনকোডারের ব্লক চিত্র  

যেকোনো মুহূর্তে আঁটটি ইনপুটের মধ্যে একটি মাত্র ইনপুট ১ এবং বাকি সকল ইনপুট ০ থাকে। নিচে 8 to 3 লাইন এনকোডারের সত্যক সারণি দেখানো হলো-

চিত্রঃ 8 to 3 লাইন এনকোডারের সত্যক সারণি

সত্যক সারণি থেকে প্রত্যেকটি আউটপুটের জন্য নিমোক্ত বুলিয়ান ফাংশন লিখা যায়-

X = D4+D5+D6+D7 

Y = D2+D3+D6+D7  

Z = D1+D3+D5+D7  

চার ইনপুট বিশিষ্ট OR গেইট ব্যবহার করে উপরের ফাংশন তিনটি বাস্তবায়ন করা যায়। নিচে 8 to 3 লাইন এনকোডারের সার্কিট দেখানো হলো-

চিত্রঃ 8 to 3 লাইন এনকোডারের সার্কিট

উপরের সার্কিটটি তিনটি OR গেইটের সমন্বয়ে তৈরি, যা আঁটটি ইনপুটকে তিন বিটে এনকোড করতে পারে।

 

সীমাবদ্ধতাঃ 

• যখন এনকোডারের সকল ইনপুট শূন্য হয়, তখন আউটপুট নির্ধারণ করতে পারে না।
• যদি একইসময় একাধিক ইনপুট সক্রিয় থাকে, তখন এনকোডারটি একটি আউটপুট দেয়, যা সঠিক নাও হতে পারে।

সুতরাং, এই সমস্যাগুলি কাটিয়ে উঠতে এনকোডার প্রতিটি ইনপুটের জন্য প্রায়োরিটি(অগ্রাধিকার) সেট করা উচিত। তারপরে, এনকোডারটির আউটপুট হবে সক্রিয় ইনপুটগুলির মধ্য যার উচ্চতর প্রায়োরিটি(অগ্রাধিকার ) রয়েছে তার জন্য।

 

এনকোডারের ব্যবহার:

• এনকোডার আলফানিউমেরিক কোডকে ASCII ও EBCDIC কোডে রূপান্তর করে।
• দশমিক সংখ্যাকে বিভিন্ন কোডে রূপান্তর করে।
• এনকোডারের সাহায্যে দশমিক সংখ্যাকে সমতুল্য বাইনারি সংখ্যায় রূপান্তর করা যায়।

 

 

ডিকোডারঃ ডিকোডার এক ধরনের সমবায় সার্কিট বা ডিজিটাল বর্তনী যা কম্পিউটার বা ডিজিটাল সিস্টেমের বোধগম্য কোডকে মানুষের বোধগম্য ফরম্যাটে রূপান্তরিত করে।

অন্যভাবে বলা যায় এটি একটি ডিজিটাল বর্তনী যা ডিকোডিং এর জন্য ব্যবহৃত হয়। অর্থাৎ ডিকোডার ডিজিটাল সিগন্যালকে অ্যানালগ সিগন্যালে রূপান্তরিত করে।

ডিকোডারের বৈশিষ্ট্যসমূহঃ

• এ বর্তনীর n সংখ্যক ইনপুট লাইন থেকে সর্বাধিক 2n সংখ্যক আউটপুট লাইন পাওয়া যায়।
• যেকোনো মুহূর্তে একটি মাত্র আউটপুট লাইনের মান ১ হয় এবং বাকি সকল আউটপুট লাইনের মান ০ হয়। কখন কোনো আউটপুট লাইনের মান ১ হবে তা নির্ভর করে ইনপুটগুলোর মানের উপর।
• ডিকোডার এনকোডারের বিপরীত কাজ সম্পাদন করে।
• ডিকোডার সাধারণত আউটপুট ডিভাইস অর্থাৎ ডিসপ্লে ইউনিটের সাথে যুক্ত থাকে।

চিত্রঃ ডিকোডারের ব্লক চিত্র

2 to 4 লাইন ডিকোডার:

ধরি 2 to 4 লাইন  ডিকোডারের দুটি ইনপুট X ও Y এবং চারটি আউটপুট D0, D1, D2 ও D3। নিচে 2 to 4 লাইন ডিকোডারের ব্লক চিত্র দেখানো হলো-

চিত্রঃ 2 to 4 লাইন ডিকোডারের ব্লক চিত্র

যেকোনো মুহূর্তে চারটি আউটপুটের মধ্যে একটি মাত্র আউটপুট ১ এবং বাকি সকল আউটপুট ০ থাকে। নিচে 2 to 4 লাইন ডিকোডারের সত্যক সারণি দেখানো হলো-

চিত্রঃ 2 to 4 লাইন ডিকোডারের সত্যক সারণি 

সত্যক সারণি থেকে SOP মেথডের সাহায্যে প্রত্যেকটি আউটপুটের জন্য নিমোক্ত বুলিয়ান ফাংশন লিখা যায়-

প্রতিটি আউটপুটে একটি করে মোট চারটি প্রোডাক্ট টার্ম আছে। অর্থাৎ চারটি AND গেইটের সাহায্যে চারটি প্রোডাক্ট টার্ম বাস্তবায়ন করা যাবে। নিচে 2 to 4 লাইন ডিকোডারের সার্কিট দেখানো হলো-

চিত্রঃ 2 to 4 লাইন ডিকোডারের সার্কিট 

3 to 8 লাইন ডিকোডার:

ধরি 3 to 8 লাইন  ডিকোডারের তিনটি ইনপুট X , Y ও Z এবং আঁটটি আউটপুট D0 to  D7। নিচে 3 to 8 লাইন ডিকোডারের ব্লক চিত্র দেখানো হলো-

চিত্রঃ 3 to 8 লাইন ডিকোডারের ব্লক চিত্র

যেকোনো মুহূর্তে আঁটটি আউটপুটের মধ্যে একটি মাত্র আউটপুট ১ এবং বাকি সকল আউটপুট ০ থাকে। নিচে 3 to 8 লাইন ডিকোডারের সত্যক সারণি দেখানো হলো-

চিত্রঃ 3 to 8 লাইন ডিকোডারের সত্যক সারণি 

সত্যক সারণি থেকে SOP মেথডের সাহায্যে প্রত্যেকটি আউটপুটের জন্য নিমোক্ত বুলিয়ান ফাংশন লিখা যায়-

প্রতিটি আউটপুটে একটি করে মোট আঁটটি প্রোডাক্ট টার্ম আছে। অর্থাৎ আঁটটি AND গেইটের সাহায্যে আঁটটি প্রোডাক্ট টার্ম বাস্তবায়ন করা যাবে। নিচে 3 to 8 লাইন ডিকোডারের সার্কিট দেখানো হলো-

চিত্রঃ 3 to 8 লাইন ডিকোডারের সার্কিট

 

ডিকোডারের ব্যবহার:

• কম্পিউটারে ব্যবহৃত কোডকে মানুষের বোধগম্য ফরম্যাটে রূপান্তর করতে।
• জটিল কোডকে সহজ কোডে রূপান্তর করতে।
• ডিসপ্লে ইউনিটে।
• বাইনারি সংখ্যাকে সমতুল্য দশমিক সংখ্যায় রূপান্তর করতে।
• ডেটা মাল্টিপ্লেক্সিং ও ডিমাল্টিপ্লেক্সিং এর ক্ষেত্রে।

 

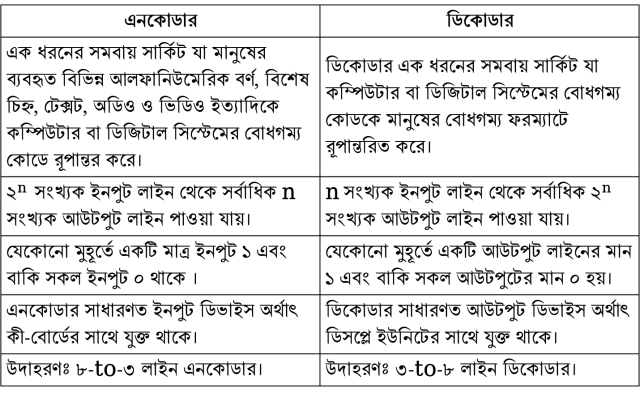
এনকোডার ও ডিকোডারের মধ্যে পার্থক্যঃ 

অ্যাডার সার্কিট (Adder Circuit) বা যোগের বর্তনী: যে সমবায় সার্কিট দ্বারা যোগের কাজ সম্পন্ন হয় তাকে অ্যাডার বা যোগের বর্তনী বলে।

কম্পিউটারের সকল গাণিতিক কাজ বাইনারি যোগের মাধ্যমে সম্পন্ন হয়। গুণ হলো বার বার যোগ করা এবং ভাগ হলো বার বার বিয়োগ করা। আবার পূরক পদ্ধতিতে বাইনারি যোগের মাধ্যমেই বিয়োগ করা যায়। কাজেই যোগ করতে পারা মানেই হলো গুণ, বিয়োগ এবং ভাগ করতে পারা। অ্যাডার সার্কিট দুই ধরনের। যথা:

• হাফ অ্যাডার সার্কিট (Half Adder Circuit) বা অর্ধ যোগের বর্তনী
• ফুল অ্যাডার সার্কিট (Full Adder Circuit) বা পূর্ণ যোগের বর্তনী

হাফ অ্যাডার সার্কিট (অর্ধ যোগের বর্তনী): যে সমবায় সার্কিট দুটি বিট যোগ করে একটি যোগফল(S) ও একটি ক্যারি(C) আউটপুট দেয় তাকে হাফ অ্যাডার সার্কিট বা অর্ধযোগের বর্তনী বলে।

চিত্রঃ হাফ অ্যাডারের ব্লক চিত্র 

হাফ অ্যাডার দুটি বিট যোগ করতে পারে। সুতরাং দুটি বিট দিয়ে চার ধরনের ভিন্ন ভিন্ন ইনপুট সেট তৈরি করা যায়। নিম্নে ভিন্ন ভিন্ন চার ধরনের ইনপুট সেট এর জন্য আউটপুট সত্যক সারণিতে দেখানো হলো-

চিত্রঃ হাফ অ্যাডারের সত্যক সারণি 

হাফ অ্যাডারের সত্যক সারণি থেকে দেখতে পাই আউটপুট sum হলো Exclusive-OR গেইট এর আউটপুট এবং আউটপুট carry হলো AND গেইট এর আউটপুট।  সুতরাং হাফ অ্যাডারের বুলিয়ান এক্সপ্রেশন হলো- 

sum এর ক্ষেত্রে-

S = A XOR B = A ⊕ B

carry এর ক্ষেত্রে-

C= A AND B = A.B

sum এবং carry এর বুলিয়ান এক্সপ্রেশন ব্যবহার করে হাফ অ্যাডারের সার্কিট 

চিত্রঃ হাফ অ্যাডারের সার্কিট 

শুধুমাত্র  মৌলিক গেইট ব্যবহার করে হাফ অ্যাডার এর লজিক সার্কিটঃ 

হাফ অ্যাডারের সত্যক সারণি থেকে SOP নিয়মানুসারে sum এবং carry এর নিম্নরূপ বুলিয়ান এক্সপ্রেশন পাওয়া যায়-  

sum এবং carry এর বুলিয়ান এক্সপ্রেশন ব্যবহার করে হাফ অ্যাডারের সার্কিট 

চিত্রঃ হাফ অ্যাডারের সার্কিট (শুধুমাত্র মৌলিক গেইটের সাহায্যে) 

 

• শুধুমাত্র NAND গেইটের সাহায্যে হাফ-অ্যাডারের সার্কিট তৈরি বা বাস্তবায়ন কর। 
• শুধুমাত্র NOR গেইটের সাহায্যে হাফ-অ্যাডারের সার্কিট তৈরি বা বাস্তবায়ন কর।

হাফ অ্যাডারের অসুবিধা:

হাফ অ্যাডার সার্কিটের একটি বড় অসুবিধা হলো যখন এটি বাইনারি অ্যাডার হিসাবে ব্যবহৃত হয়, কারণ একাধিক ডেটা বিট যোগ করার সময় পূর্ববর্তী সার্কিট থেকে “ক্যারি-ইন” করার বিধান নেই।

উদাহরণস্বরূপ, আমরা দুটি ৮-বিটের ডেটা একসাথে যুক্ত করতে চাই , এক্ষেত্রে ফলাফলে যে কোন ক্যারি বিটকে পরবর্তী ধাপে “রিপল” বা যুক্ত করতে সক্ষম হতে হবে।
হাফ অ্যাডার সবচেয়ে জটিল ক্রিয়াকলাপটি করতে পারে “1 + 1”, কিন্তু হাফ অ্যাডারে কোনও ক্যারি ইনপুট না
থাকায় ফলাফলটি ভুল হবে। এই সমস্যাটি কাটিয়ে ওঠার একটি সহজ উপায় হল বাইনারি অ্যাডার হিসাবে ফুল অ্যাডার সার্কিট ব্যবহার করা।  

 

ফুল অ্যাডার সার্কিট (পূর্ণ যোগের বর্তনী): যে সমবায় সার্কিট তিনটি বাইনারি বিট (দুটি ইনপুট বিট ও একটি ক্যারি বিট) যোগ করে একটি যোগফল(S) এবং বর্তমান ক্যারি(C0) আউটপুট দেয় তাকে ফুল অ্যাডার সার্কিট বা পূর্ণ যোগের বর্তনী বলে। ক্যারিসহ অপর দুটি বিট যোগ করার জন্য ফুল অ্যাডার সার্কিট ব্যবহৃত হয়। আবার দুটি হাফ অ্যাডার সার্কিট দ্বারা একটি ফুল অ্যাডারের কাজ করা যায়।

চিত্রঃ ফুল অ্যাডারের ব্লক চিত্র 

ফুল অ্যাডার তিনটি বিট যোগ করতে পারে। সুতরাং তিনটি বিট দিয়ে আট ধরণের ভিন্ন ভিন্ন ইনপুট সেট তৈরি করা যায়। নিম্নে ভিন্ন ভিন্ন আট ধরনের ইনপুট সেট এর জন্য আউটপুট সত্যক সারণিতে দেখানো হলো-

চিত্রঃ ফুল অ্যাডারের সত্যক সারণি 

ফুল অ্যাডারের সত্যক সারণি থেকে SOP নিয়মানুসারে sum এবং carry এর নিম্নরূপ বুলিয়ান এক্সপ্রেশন পাওয়া যায়-  

ফুল অ্যাডারের sum এবং carry এর বুলিয়ান এক্সপ্রেশন ব্যবহার করে সার্কিট 

চিত্রঃ ফুল অ্যাডারের সার্কিট ( শুধুমাত্র মৌলিক গেইটের সাহায্যে ) 

ফুল অ্যাডারের বুলিয়ান এক্সপ্রেশনদুটি সরলীকরণ করে পাই-

  

ফুল অ্যাডারের sum এবং carry এর সরলীকৃত এক্সপ্রেশনদুটি ব্যবহার করে সার্কিট 

চিত্রঃ ফুল অ্যাডারের সার্কিট ( সরলীকৃত সমীকরণের ) 

 

• শুধুমাত্র NAND গেইটের সাহায্যে ফুল অ্যাডারের সার্কিট তৈরি বা বাস্তবায়ন কর। 
• শুধুমাত্র NOR গেইটের সাহায্যে ফুল অ্যাডারের সার্কিট তৈরি বা বাস্তবায়ন কর। 

 

হাফ অ্যাডার সার্কিটের সাহায্যে ফুল অ্যাডার সার্কিট বাস্তবায়ন: 

আমরা জানি, ফুল অ্যাডারের ইনপুট A, B ও Ci  এবং আউটপুট যোগফল S ও ক্যারি Co হলে ফুল অ্যাডারের ক্ষেত্রে,

S = AꚚBꚚCi

Co=(AꚚB).Ci + A.B

উপরের ফাংশনদুটি বাস্তবায়নের লক্ষে দুটি হাফ অ্যাডার ও একটি অর গেইটের সাহায্যে নিমোক্ত সার্কিট তৈরি করা হলো-

চিত্রঃ হাফ অ্যাডারের সাহায্যে ফুল অ্যাডারের সার্কিট বাস্তবায়ন 

প্রথম হাফ অ্যাডারের ক্ষেত্রে-

S1=AꚚB  এবং

C1=A.B

দ্বিতীয় হাফ অ্যাডারের ক্ষেত্রে-

S2=S1ꚚCi এবং

C2=S1.Ci

S2=S1ꚚCi  এই সমীকরণে S1=AꚚB বসিয়ে পাই S2= AꚚBꚚCi  যা ফুল-অ্যাডারের যোগফল S ।

আবার Co=C1+C2 সমীকরণে C1 ও C2 এর মান বসিয়ে পাই Co=(AꚚB).Ci + A.B  যা ফুল-অ্যাডারের আউটপুট ক্যারি Co । সুতরাং দুটি হাফ অ্যাডার ও একটি অর গেইটের সাহায্যে একটি ফুল অ্যাডার বাস্তবায়ন সম্ভব।

 

বাইনারি অ্যাডারঃ যে অ্যাডার দুটি বাইনারি সংখ্যা যোগ করতে পারে তাকে বাইনারি অ্যাডার বলে। বাইনারি অ্যাডার দুই প্রকার। যথা-

• প্যারালাল বাইনারি অ্যাডার
• সিরিয়াল বাইনারি অ্যাডার

প্যারালাল বাইনারি অ্যাডারঃ প্যারালাল বাইনারি অ্যাডার n বিটের দুইটি বাইনারি সংখ্যার বিটগুলোকে সমান্তরালে যোগ করতে পারে। শুধুমাত্র ফুল-অ্যাডার অথবা হাফ-অ্যাডার এবং ফুল-অ্যাডারের সাহায্যে প্যারালাল বাইনারি অ্যাডার সার্কিট তৈরি করা যায়। প্যারালাল বাইনারি অ্যাডার দিয়ে n বিটের দুইটি বাইনারি সংখ্যা যোগ করার জন্য একটি হাফ-অ্যাডার ও (n-1) সংখ্যক ফুল-অ্যাডার ব্যবহৃত হয়। তবে n বিটের দুইটি বাইনারি সংখ্যার যোগ শুধুমাত্র n সংখ্যক ফুল-অ্যাডার ব্যবহার করেও করা যায়। এক্ষেত্রে প্রথম ফুল অ্যাডারের ইনপুট ক্যারিটি গ্রাউন্ডেড (ক্যারি জিরো) করে রাখা হয়।

প্যারালাল বাইনারি অ্যাডার বা বাইনারি অ্যাডারের সাহায্যে দুইটি বাইনারি সংখ্যা A4A3A2A1 এবং B4B3B2B1 এর যোগঃ

হাফ-অ্যাডার এবং ফুল-অ্যাডার ব্যবহার করে:   

চিত্রঃ ৪-বিট বাইনারি প্যারালাল অ্যাডার 

শুধুমাত্র ফুল অ্যাডার ব্যবহার করে:   

চিত্রঃ ৪-বিট বাইনারি প্যারালাল অ্যাডার 

 

উদাহরণ-১: বাইনারি অ্যাডার সার্কিটের সাহায্যে 1101 এবং 1110 যোগ।

সুতরাং (1101)2 + (1110)2 = (11011)2

 

উদাহরণ-2: বাইনারি অ্যাডার সার্কিটের সাহায্যে 11011 এবং 10101 যোগ কর।

উদাহরণ-3: বাইনারি অ্যাডার সার্কিটের সাহায্যে 110 এবং 111 যোগ কর।

 

সিরিয়াল বাইনারি অ্যাডারঃ সিরিয়াল বাইনারি অ্যাডার n বিটের দুইটি বাইনারি সংখ্যার বিটগুলোকে বিট-বাই-বিট যোগ করে থাকে। একটি ফ্লিপ-ফ্লপ এবং একটি ফুল-অ্যাডার দিয়ে সিরিয়াল বাইনারি অ্যাডার সার্কিট তৈরি করা যায়। প্রতিটি ক্লক পালসে ফুল অ্যাডার সার্কিট দুইটি বাইনারি সংখ্যার একটি করে বিট যোগ করে sum এবং আউটপুট carry দেয়। পরবর্তী ক্লক পালসে পূর্ববর্তী আউটপুট ক্যারি এবং পরবর্তী দুইটি বিট যোগ করে  sum এবং আউটপুট carry দেয়। এইভাবে n বিটের দুইটি বাইনারি সংখ্যার বিটগুলোকে বিট-বাই-বিট যোগ করে থাকে।

রেজিস্টার: রেজিস্টার হলো একগু‛ছ ফ্লিপ-ফ্লপ এবং গেইটের সমন্বয়ে গঠিত সার্কিট যা অস্থায়ী মেমরি হিসেবে কাজ করে। এর প্রত্যেকটি ফ্লিপ-ফ্লপ একটি করে বাইনারি বিট সংরক্ষণ করতে পারে। কেন্দ্রীয় প্রক্রিয়াকরণ অংশে প্রোগ্রাম নির্বাহের সময় উপাত্ত অস্থায়ীভাবে জমা রাখার জন্য রেজিস্টার ব্যবহৃত হয়। n বিটের একটি বাইনারি তথ্য ধারণের জন্য n সংখ্যক ফ্লিপ-ফ্লপ বিশিষ্ট একটি রেজিস্টার প্রয়োজন। ৮-বিট রেজিস্টার, ১৬- বিট রেজিস্টার, ৩২-বিট রেজিস্টার ইত্যাদি- যারা যথাক্রমে ৮, ১৬, ৩২ বিট তথ্য ধারণ করতে পারবে।

• রেজিস্টারের প্রকারভেদ-
  গঠন অনুসারে রেজিস্টার বিভিন্ন প্রকার হতে পারে। যথা:
  ১. প্যারালাল লোড রেজিস্টার 
  ২. শিফ্ট রেজিস্টার 
  কাজের প্রকৃতি অনুসারে রেজিস্টার বিভিন্ন প্রকার হতে পারে। যথা:
  ১. অ্যাকিউমুলেটর রেজিস্টার 
  ২. সাধারণ রেজিস্টার 
  ৩. বিশেষ রেজিস্টার 

প্যারালাল লোড রেজিস্টার: একটি সাধারণ প্যারালাল লোড রেজিস্টার বা বাফার রেজিস্টারের ব্লক ডায়াগ্রাম দেখানো হলো। এটি ৪ বিটের বাইনারি তথ্য সংরক্ষণ করতে পারে। প্যারালাল লোড রেজিস্টার হলো এমন এক ধরনের রেজিস্টার যেখানে একটি কমন পালস্ সিস্টেম থাকে। কমন পালসের যেকোনো একটি টার্মিনাল পাল্স পাবার সাথে সাথে সবগুলো রেজিস্টার সক্রিয় হয় এবং তথ্য ধারণ করে।

শিফ্ট রেজিস্টারঃ যে রেজিস্টার বাইনারি বিট ধারণের পাশাপাশি ধারনকৃত বিটকে ডানদিকে বা বামদিকে বা উভয় দিকে সরাতে পারে তাকে শিফ্ট রেজিস্টার বলে। শিফট রেজিস্টারে ফ্লিফ-ফ্লপগুলো চেইন আকারে একটির আউটপুট আরেকটির ইনপুটের সাথে সংযুক্ত থাকে। একটি কমন পাল্সের মাধ্যমে সব ফ্লিপ-ফ্লপ ইনপুট গ্রহণ করে এক স্টেট হতে অপর স্টেটে ডেটা শিফটিং এর কাজ করে।

রেজিস্টারের ব্যবহারঃ রেজিস্টার হলো CPU এর অন্তর্গত সঞ্চয় ব্যবস্থা। এতে তথ্য বা নির্দেশ সাময়িকভাবে সঞ্চিত রাখা যায়। রেজিস্টারে প্রোগ্রামার কোনো কিছু জমা রাখতে পারে না, একমাত্র CPU-ই গণনার প্রয়োজনে রেজিস্টারে কোনো কিছু সঞ্চিত রাখতে পারে। রেজিস্টারের গঠন প্রধান মেমরির অনুরূপ। বিভিন্ন ধরনের প্রিন্টারে রেজিস্টার ব্যবহৃত হয়, কী-বোর্ড বাফারে ব্যবহৃত হয়।

কাউন্টারঃ কাউন্টার হলো এমন একটি সিকুয়েন্সিয়াল ডিজিটাল ইলেকট্রনিক্স সার্কিট যা  ফ্লিপ-ফ্লপ এবং লজিক গেইট দিয়ে গঠিত এবং তাতে দেয়া ইনপুট পালসের সংখ্যা গুণতে পারে। যে কাউন্টার বাইনারি সিকুয়েন্স অনুসরণ করে তাকে বাইনারি কাউন্টার বলে। একটি কাউন্টার কত থেকে
কত গণনা করবে তা কাউন্টার এর ডিজাইনের উপর নির্ভর করে। সুতরাং, একটি n বিট বাইনারি কাউন্টার 0 থেকে 2n -1 পর্যন্ত পর্যায়ক্রমিক গুণতে পারে।

মোড নাম্বার/মডিউলাসঃ  কাউন্টারের মোড নাম্বার বা মডিউলাস হলো কাউন্টারটি সর্বো‛চ কত সংখ্যা গুণতে পারে। যদি কোনোএকটি কাউন্টারের বিট সংখ্যা n হয় তবে এটি n টি ফ্লিপ-ফ্লপ নিয়ে তৈরি হবে এবং তা সিকুয়েন্সিয়াল বা ধারাবাহিকভাবে 0 থেকে 2n -1 সংখ্যক সংখ্যা গণনা করতে পারবে। অর্থাৎ n বিট কাউন্টারের মডিউলাস সংখ্যা 2n। তবে কাউন্টারের ফ্লিপ-ফ্লপের সংখ্যা হ্রাস-বৃদ্ধি করে মডিউলাসের সংখ্যা হ্রাস-বৃদ্ধি করা যায়।

কাউন্টারের প্রকারভেদ:

কাউন্টারের ব্যবহার:

• ১. ক্লক পালসের সংখ্যা গণনার জন্য
  ২. টাইমিং সিগন্যাল প্রদানের জন্য
  ৩. ডিজিটাল কম্পিউটারে
  ৪. ডিজিটাল ঘড়িতে
  ৫. বৈদ্যুতিক স্পন্দন গণনার ক্ষেত্রে
  ৬. প্যারালাল ডেটাকে সিরিয়াল ডেটায় রূপান্তর করতে।